Deterministic Optimal Consumption-Investment Model
Contents
Deterministic Optimal Consumption-Investment Model¶
Randall Romero Aguilar, PhD
This demo is based on the original Matlab demo accompanying the Computational Economics and Finance 2001 textbook by Mario Miranda and Paul Fackler.
Original (Matlab) CompEcon file: demdoc01.m
Running this file requires the Python version of CompEcon. This can be installed with pip by running
!pip install compecon --upgrade
Last updated: 2021-Oct-01
About¶
Utility maximizing agent must decide how much to consume and how much to hold in a riskless asset.
State
w stock of wealth
Control
q consumption rate
Parameters
theta relative risk aversion
r continuous rate of return on asset
rho continuous discount rate
Preliminary tasks¶
import pandas as pd
import matplotlib.pyplot as plt
from compecon import ODE
Initial state and time horizon¶
winit = 1 # initial capital stock
T = 50 # time horizon
SOLUTION & SIMULATION \(r>\rho\)¶
Model parameters¶
𝜃 = 2.0 # relative risk aversion
r = 0.08 # continuous rate of return on asset
𝜌 = 0.05 # continuous discount rate
# V'>0 iff V''<0 iff sign>0 where
sign = 𝜌 - r*(1-𝜃)
if sign<0:
print('Invalid Parameters')
Solve ODE¶
g = lambda w: ((r-𝜌)/𝜃)*w
problem1 = ODE(g, T, [winit])
problem1.rk4(xnames=[r"$r>\rho$"])
PARAMETER xnames NO LONGER VALID. SET labels= AT OBJECT CREATION
SOLUTION & SIMULATION \(r<\rho\)¶
Model Parameters¶
𝜃 = 2.0 # relative risk aversion
r = 0.05 # continuous rate of return on asset
𝜌 = 0.08 # continuous discount rate
# Assume theta>0. Then V'>0 iff V''<0 iff sign>0 where
sign = 𝜌 - r*(1-𝜃)
if sign<0:
print('Invalid Parameters')
Solve ODE¶
g = lambda w: ((r-𝜌)/𝜃)*w
problem2 = ODE(g, T, [winit])
problem2.rk4(xnames=[r"$r<\rho$"])
PARAMETER xnames NO LONGER VALID. SET labels= AT OBJECT CREATION
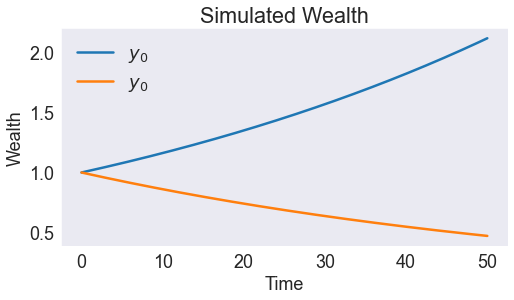
PLOT SOLUTIONS¶
# Plot optimal wealth path
fig, ax= plt.subplots(figsize=[8,4])
wealth = pd.concat([problem1.x, problem2.x], axis=1)
wealth.plot(ax=ax)
ax.set(title='Simulated Wealth',
xlabel='Time',
ylabel='Wealth');