Computing Function Inner Products, Norms & Metrics
Contents
Computing Function Inner Products, Norms & Metrics¶
Randall Romero Aguilar, PhD
This demo is based on the original Matlab demo accompanying the Computational Economics and Finance 2001 textbook by Mario Miranda and Paul Fackler.
Original (Matlab) CompEcon file: demmath02.m
Running this file requires the Python version of CompEcon. This can be installed with pip by running
!pip install compecon --upgrade
Last updated: 2022-Oct-23
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-dark')
import scipy.integrate as integrate
import scipy as sp
Class function¶
We now define the class function. An object of class function operates just as a lambda function, but it supports several function operations: sum, substraction, multiplication, division, power, absolute value, integral, norm, and angle.
This example illustrates how it is possible to overwrite the methods of the function class.
class function:
def __init__(self, func):
self.f = func
def __call__(self, *args):
return self.f(*args)
def __add__(self, other):
return function(lambda *args: self.f(*args) + other.f(*args))
def __sub__(self, other):
return function(lambda *args: self.f(*args) - other.f(*args))
def __mul__(self, other):
return function(lambda *args: self.f(*args) * other.f(*args))
def __pow__(self, n):
return function(lambda *args: self.f(*args) ** n)
def __truediv__(self, other):
return function(lambda *args: self.f(*args) / other.f(*args))
def integral(self, l, h):
return integrate.quad(self.f, l, h)[0]
def abs(self):
return function(lambda *args: np.abs(self.f(*args)))
def norm(self, l, h, p=2):
return ((self.abs()) ** p).integral(l, h) ** (1/p)
def angle(self, other, l, h):
fg = (self * other).integral(l, u)
ff = (self**2).integral(l, u)
gg = (other**2).integral(l, u)
return np.arccos(fg*np.sqrt(ff*gg))*180/np.pi
Compute inner product and angle¶
Define the functions \(f(x) = 2x^2-1\) and \(g(x)= 4x^3-3x\), both over the domain \([-1,1]\). Compute their inner product and angle.
l, u = -1, 1
f = function(lambda x: 2 * x**2 - 1)
g = function(lambda x: 4 * x**3 - 3*x)
fg = (f*g).integral(l, u)
ff = (f**2).integral(l, u)
gg = (g**2).integral(l, u)
angle = f.angle(g, l, u)
print(f'∫(f*g)(x)dx = {fg:.2f}')
print(f'∫(f^2)(x)dx = {ff:.2f}')
print(f'∫(g^2)(x)dx = {gg:.2f}')
print(f'Angle in degrees = {angle:.0f}°')
∫(f*g)(x)dx = 0.00
∫(f^2)(x)dx = 0.93
∫(g^2)(x)dx = 0.97
Angle in degrees = 90°
Compute Function Norm¶
Now compute the norm of function \(f(x) = x^2 - 1\) over the domain \([0, 2]\).
l, u = 0, 2
f = function(lambda x: x ** 2 - 1)
print(f'∥f∥₁ = {f.norm(l, u, 1):.3f}')
print(f'∥f∥₂ = {f.norm(l, u, 2):.3f}')
∥f∥₁ = 2.000
∥f∥₂ = 1.751
Compute function metrics¶
l, u = 0, 1
f = function(lambda x: 5 + 5*x**2)
g = function(lambda x: 4 + 10*x - 5*x**2)
print(f'∥f-g∥₁ = {(f-g).norm(l, u, 1):.3f}')
print(f'∥f-g∥₂ = {(f-g).norm(l, u, 2):.3f}')
∥f-g∥₁ = 0.883
∥f-g∥₂ = 1.000
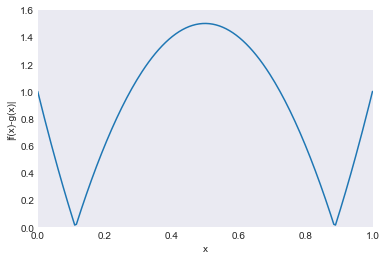
Illustrate Function metrics¶
x = np.linspace(l,u,200)
fig, ax = plt.subplots()
ax.set(xlabel='x',
ylabel='|f(x)-g(x)|',
xlim=[0, 1],
ylim=[0, 1.6])
plt.plot(x, (f-g).abs()(x))
[<matplotlib.lines.Line2D at 0x29143fc8610>]
Demonstrate Pythagorean Theorem¶
Again, define the functions \(f(x) = 2x^2-1\) and \(g(x)= 4x^3-3x\), both over the domain \([-1,1]\).
l,u = -1, 1
f = function(lambda x: 2 * x**2 - 1)
g = function(lambda x: 4 * x**3 - 3*x)
ifsq = (f**2).integral(l,u)
igsq = (g**2).integral(l,u)
ifplusgsq = ((f+g)**2).integral(l,u)
print(f'∫f²(x)dx = {ifsq:.4f}')
print(f'∫g²(x)dx = {igsq:.4f}')
print(f'∫(f+g)²(x)dx = {ifplusgsq:.4f}')
∫f²(x)dx = 0.9333
∫g²(x)dx = 0.9714
∫(f+g)²(x)dx = 1.9048
