Sparse linear equations

Sparse linear equations

Randall Romero Aguilar, PhD

This demo is based on the original Matlab demo accompanying the Computational Economics and Finance 2001 textbook by Mario Miranda and Paul Fackler.

Original (Matlab) CompEcon file: demlin03.m

Running this file requires the Python version of CompEcon. This can be installed with pip by running

!pip install compecon --upgrade

Last updated: 2022-Ago-19

import numpy as np
import pandas as pd
from numpy.linalg import solve
from scipy.sparse.linalg import spsolve
from timeit import default_timer as timer
import matplotlib.pyplot as plt
from scipy.sparse import csc_matrix
np.set_printoptions(precision=4)
plt.style.use('seaborn-dark')
plt.style.use('seaborn-talk')

Define some timing functions

tic = lambda: timer()
toc = lambda t: timer() - t

Compute the time to solve a system of equations, for full and sparce matrices

N, M = 800, 100

AA = np.random.rand(N, N)
bb = np.random.rand(N, 1)
for i in range(N):
    for j in range(N):
        if abs(i - j) > 1:
            AA[i,j] = 0

nvalues = np.arange(20,N+1,30)
times = pd.DataFrame(index=nvalues, columns=['Using full matrix','Using sparse matrix'])
times.index.name='n'

for n in nvalues:
    A = AA[:n, :n]
    b = bb[:n]
    tt = tic()
    for i in range(M):
        x = solve(A, b)

    toc1 = toc(tt)

    S = csc_matrix(A)
    tt = tic()
    for i in range(M):
        x = spsolve(S, b)

    toc2 = toc(tt)
    times.loc[n] = toc1, toc2

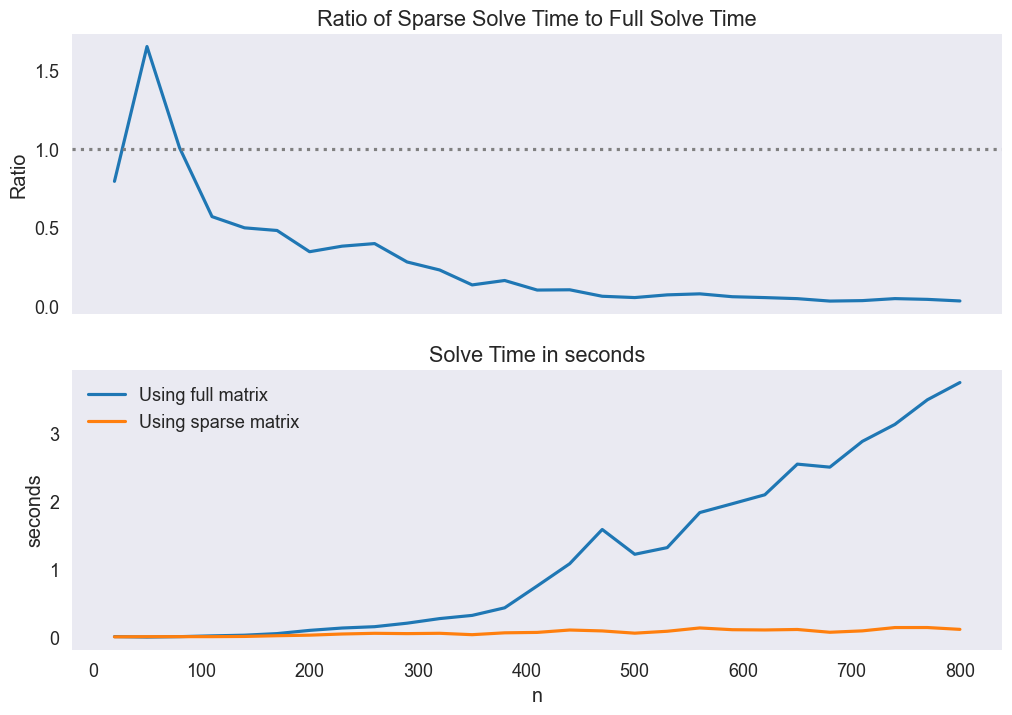
Plot effort ratio

times['Ratio'] = times['Using sparse matrix'] / times['Using full matrix']

fig, axs = plt.subplots(2, 1, figsize=[12, 8], sharex=True)
times['Ratio'].plot(ax=axs[0])
axs[0].set(ylabel='Ratio', 
           title='Ratio of Sparse Solve Time to Full Solve Time')
axs[0].axhline(1.0, color='gray', linestyle=':')           

times[['Using full matrix', 'Using sparse matrix']].plot(ax=axs[1])
axs[1].set(ylabel='seconds', 
           title='Solve Time in seconds')

[Text(0, 0.5, 'seconds'), Text(0.5, 1.0, 'Solve Time in seconds')]
../../_images/03 Sparse linear equations_7_1.png 
times
Using full matrix Using sparse matrix Ratio
n
20 0.015677 0.012451 0.794241
50 0.008911 0.014726 1.652557
80 0.015079 0.015211 1.00878
110 0.02672 0.015222 0.569671
140 0.036531 0.018197 0.498118
170 0.05988 0.028821 0.481304
200 0.107153 0.03708 0.34605
230 0.141798 0.054089 0.381452
260 0.161393 0.064216 0.397887
290 0.212905 0.059762 0.2807
320 0.280219 0.064393 0.229795
350 0.327173 0.044081 0.134732
380 0.438411 0.071409 0.162882
410 0.759178 0.077416 0.101974
440 1.085809 0.112562 0.103666
470 1.588059 0.099183 0.062455
500 1.224117 0.0663 0.054161
530 1.322073 0.094321 0.071343
560 1.836372 0.142978 0.077859
590 1.965873 0.117131 0.059582
620 2.097353 0.1133 0.05402
650 2.547172 0.120363 0.047253
680 2.502875 0.079582 0.031796
710 2.881523 0.100067 0.034727
740 3.130402 0.148704 0.047503
770 3.491733 0.149018 0.042677
800 3.744745 0.121962 0.032569

previous

Ill-conditioning of Vandermonde matrix

next

Nonlinear Equations