Clases y objetos
Contents
Clases y objetos#
Diseñando una clase#
Una clases es una plantilla que describe las propiedades que caracterizan a un objeto. Cada clases contiene datos (miembros) y funciones (métodos) que operan sobre los objetos.
Para referirnos a los miembros y métodos de una clase utilizamos la notación punto: escribimos el nombre del objeto seguido de un punto y del miembro o método deseado.
Ejemplo 1: una cuenta bancaria#
En este ejemplo creamos una clase para representar una cuenta bancaria.
Los miembros que debe guardar un objeto de esta clase son:
clientesaldonúmerofecha_apertura
Los métodos que debe ejecutar la cuenta son
depositar()retirar()transferir()
Además, debemos implementar estos métodos:
__init__()cómo se abre una cuenta__repr__()cómo se imprime una cuenta
Finalmente, el método transferir debe verificar que la cuenta de destino exista.
from datetime import datetime
class cuenta:
total_abiertas = 0
existentes = dict()
def __init__(self, cliente):
cuenta.total_abiertas += 1
self.cliente = cliente
self.saldo = 0
self.número = f'UCR{cuenta.total_abiertas:04d}'
self.fecha_apertura = datetime.now()
cuenta.existentes[self.número] = self
print(f"Se ha abierto la cuenta {self.número} a nombre de {self.cliente} el {self.fecha_apertura}")
def __repr__(self):
return f"Cuenta {self.número}, cliente {self.cliente}, saldo = {self.saldo}"
def depositar(self, monto):
if monto < 0:
print("ERROR: monto no puede ser negativo")
else:
self.saldo += monto
print(f"Se depositó {monto} en la cuenta {self.número}. Nuevo saldo es {self.saldo}")
def retirar(self, monto):
if monto < 0:
print("ERROR: monto no puede ser negativo")
elif monto > self.saldo:
print("ERROR: fondos insuficientes")
else:
self.saldo -= monto
print(f"Se retiró {monto} en la cuenta {self.número}. Nuevo saldo es {self.saldo}")
def transferir(self, monto, otra_cuenta):
if monto < 0:
print("ERROR: monto no puede ser negativo")
elif monto > self.saldo:
print("ERROR: fondos insuficientes")
if otra_cuenta not in cuenta.existentes:
print("ERROR: cuenta destino no existe.")
else:
self.saldo -= monto
cuenta.existentes[otra_cuenta].saldo += monto
print(f"Se transfirió {monto} de la cuenta {self.número} a la cuenta {otra_cuenta}.")
Para probar la clase, abramos la cuenta cta1 a nombre de “Rodrigo” y la cuenta cta2 a nombre de “Pedro”
cta1 = cuenta("Rodrigo")
cta2 = cuenta("Pedro")
Se ha abierto la cuenta UCR0001 a nombre de Rodrigo el 2022-07-21 00:13:25.995057
Se ha abierto la cuenta UCR0002 a nombre de Pedro el 2022-07-21 00:13:25.995057
Depositamos 400 en la cuenta de “Rodrigo”
cta1.depositar(400)
cta1
Se depositó 400 en la cuenta UCR0001. Nuevo saldo es 400
Cuenta UCR0001, cliente Rodrigo, saldo = 400
Rodrigo le transfiere 200 a Pedro
cta1.transferir(200, "UCR0002")
Se transfirió 200 de la cuenta UCR0001 a la cuenta UCR0002.
Revisamos las cuentas existentes
cuenta.existentes
{'UCR0001': Cuenta UCR0001, cliente Rodrigo, saldo = 200,
'UCR0002': Cuenta UCR0002, cliente Pedro, saldo = 200}
Revisamos el saldo de Pedro
cta2.saldo
200
Rodrigo retira 200 colones.
cta1.retirar(200)
Se retiró 200 en la cuenta UCR0001. Nuevo saldo es 0
Pedro intenta retirar un monto superior a su saldo
cta2.retirar(3600)
ERROR: fondos insuficientes
Por último, volvemos a revisar las cuentas.
cuenta.existentes
{'UCR0001': Cuenta UCR0001, cliente Rodrigo, saldo = 0,
'UCR0002': Cuenta UCR0002, cliente Pedro, saldo = 200}
Ejemplo 2: un polinomio#
En este ejemplo creamos una clase para representar un polinomio.
Los miembros que debe guardar un objeto de esta clase son:
coefs= \([c_0, c_1, c_2, \dots, c_n]\)grado= \(n\)
Los métodos que debe ejecutar la cuenta son
simplificar()para eliminar los monomios de mayor grado que tengan coeficiente ceroplot()para graficar el polinomio
Además, debemos implementar estos métodos:
__init__()cómo se crea un polinomio__repr__()cómo se imprime un polinomio__add__()para sumar dos polinomios__call__()para evaluar un polinomio
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class polinomio:
def __init__(self, *coeficientes):
self.coefs = np.array(coeficientes)
self.simplificar()
self.grado = len(self.coefs) - 1
def __repr__(self):
monomios = [f"{c if c!=1 else ''}{'x' if k else ''}{f'^{k}' if k>1 else''}" for k, c in enumerate(self.coefs) if c!=0]
return ' + '.join(monomios)
def simplificar(self):
coefs = list(self.coefs)
while coefs[-1] == 0:
coefs.pop()
self.coefs = np.array(coefs)
def __add__(self, otro):
grado = max(self.grado, otro.grado)
coefs = np.zeros(1 + grado)
coefs[:self.grado+1] = self.coefs
coefs[:otro.grado+1] += otro.coefs
return polinomio( *coefs )
def __call__(self, x):
resultado = np.zeros_like(x)
for coef in self.coefs[-1:0:-1]:
resultado += coef
resultado *= x
return resultado + self.coefs[0]
def plot(self, ax, a, b, n=121, **kwargs):
x = np.linspace(a, b, n)
ax.plot(x, self(x), **kwargs)
ax.set_title(str(self))
return ax
Creamos el polinomio \(P(x)= 9 + 2x^2 +2x^3\)
P = polinomio(9, 0, 2, 2)
P
9 + 2x^2 + 2x^3
Creamos el polinomio \(Q(x) = 3 + x + x^2 -2x^3\)
Q = polinomio(3,1,1,-2)
Q
3 + x + x^2 + -2x^3
Sumamos los dos polinomios: \(R(x) = P(x) + Q(x)\)
R = P + Q
R
12.0 + x + 3.0x^2
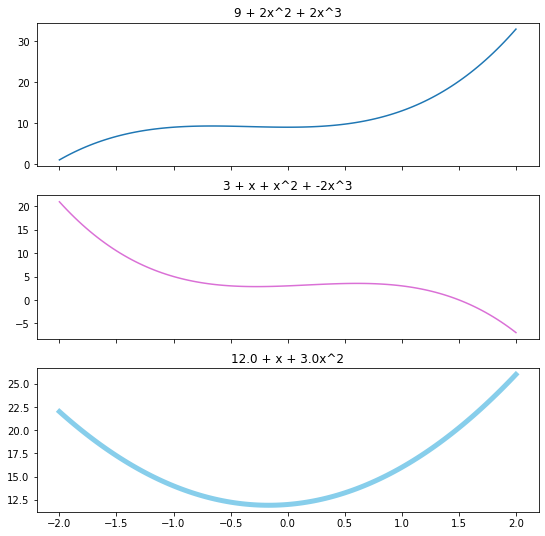
Graficamos los 3 polinomios en una figura, en el rango \(x\in[-2,2]\), cada uno en su propio eje de coordenadas.
fig, axs = plt.subplots(3,1, figsize=[9,9], sharex=True)
P.plot(axs[0], -2,2)
Q.plot(axs[1], -2,2, color='orchid')
R.plot(axs[2], -2,2, color='skyblue', linewidth=5)
<AxesSubplot:title={'center':'12.0 + x + 3.0x^2'}>
Ejemplo 3: un modelo de regresión lineal#
class RegresiónLineal:
def __init__(self, y: str, X: str, data):
X = X.split()
variables = [y] + X
datos = data[variables].dropna(how='any')
self.y = datos[[y]] # variable endógena
self.X = datos[variables] # variables exógenas
self.X.iloc[:, 0] = 1.0 # intercepto
self.residuos = np.zeros_like(self.y) # residuos
self.names = dict(X = ['intercepto'] + X, y = y) # nombres de las variables
self.nobs, self.nvar = self.X.shape # número de observaciones y de variables
def ols(self):
"""
ols: Estima una regresión lineal con mínimos cuadrados ordinarios
"""
y, X = self.y.values, self.X.values # extraer datos como arrays de numpy
xpxi = np.linalg.inv(X.T @ X) # (X'X)^{-1}
beta = xpxi @ (X.T @ y) # estimador mínimos cuadrados
yhat = X @ beta # valores ajustados
resid = y - yhat # residuos
sigu = (resid**2).sum() # sumatoria de residuos al cuadrado
sige = sigu / (self.nobs - self.nvar) # varianza estimada del término de error
bstd = np.sqrt(sige * np.diag(xpxi)) # error estándar de los coeficientes estimados
tstat = beta.T / bstd # estadístico t-Student
rsqr2 = ((y - y.mean())**2).sum() # suma de cuadrados de (desviación respecto a la media) de los datos endógenos
R2 = 1.0 - sigu * rsqr2 # estadístico R^2
as_series = lambda coef, name: pd.Series(coef.flatten(), index = self.names['X'], name=name) # función para convertir en serie (etiquetada) los parámetros estimados
self.beta = as_series(beta, 'beta')
self.bstd = as_series(bstd, 'bstd')
self.tstat = as_series(tstat, 'tstat')
self.residuos = resid
self.yhat = yhat
def resumen(self):
return pd.concat([self.beta, self.bstd, self.tstat], axis=1)
X = np.random.randn(100, 2)
e = np.random.randn(100, 1)
beta = np.array([[1.5], [0.8]])
y = 1.0 + X @ beta + e
data = pd.DataFrame(np.c_[y,X], columns = ['PIB', 'C', 'G'])
modelo = RegresiónLineal('PIB', 'C G', data)
modelo.ols()
modelo.resumen()
| beta | bstd | tstat | |
|---|---|---|---|
| intercepto | 0.961972 | 0.103920 | 9.256877 |
| C | 1.417703 | 0.101694 | 13.940838 |
| G | 0.829819 | 0.106405 | 7.798715 |


