3. Modelos AutoRegresivos de Media Móvil (ARMA)

\[ \begin{align}\begin{aligned}\require{color} \newcommand{\alert}[1]{{\color{RedOrange} #1}} \newcommand{\notation}[2]{\underset{\color{MidnightBlue}\text{#2}}{#1}} \newcommand{\simbolo}[2]{\underset{\color{MidnightBlue}#2}{#1}} \newcommand{\notationbrace}[2]{{\underbrace{#1}_{\color{MidnightBlue}\text{#2}}}} \DeclareMathOperator{\dd}{\,d\!} \DeclareMathOperator{\E}{\mathbb{E}{}} \DeclareMathOperator{\Var}{Var{}} \DeclareMathOperator{\Cov}{Cov{}} \DeclareMathOperator{\Lag}{L{}} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator{\Prob}{\mathbb{P}} \newcommand{\marginal}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\MAT}[1]{\begin{bmatrix} #1 \end{bmatrix}} \newcommand{\mat}[1]{\left[\begin{smallmatrix} #1 \end{smallmatrix}\right]}\\\begin{split}\DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\X}{\mathbf{x}} \DeclareMathOperator{\y}{\mathbf{y}} \DeclareMathOperator{\h}{\mathbf{h}} \newcommand{\stackEq}[1]{\MAT{#1_1 \\ #1_2 \\ \vdots \\ #1_M}} \newcommand{\e}{\mathbf{\epsilon}} \newcommand{\Y}{\mathbf{Y}} \newcommand{\estimator}[2]{{\hat{#1}^{\text{#2}}}} \newcommand{\estimate}[2]{\underset{(#2)}{#1}} \DeclareMathOperator{\plim}{plim} \newcommand{\PLIM}[2]{#1\xrightarrow{p} #2}\end{split}\end{aligned}\end{align} \]

• 3.1. Introducción
• 3.2. Proceso de media móvil MA(q)
• 3.3. Proceso autorregresivo AR(p)
• 3.4. Proceso autorregresivo de media móvil ARMA(p,q)
• 3.5. Estimación de modelos ARMA
• 3.6. Pronósticos con modelos ARMA
• 3.7. Referencias

En esta clase

• En esta clase aprenderemos a modelar series de tiempo en función de:

• sus valores rezagados (procesos autorregresivos)

• valores rezagados de un ruido blanco (procesos de media móvil)

• Primero estudiamos las propiedades teóricas de procesos estocásticos.

• Luego tratamos de identificar el PGD de nuestra serie a partir de sus estadísticos muestrales, comparándolos con los estadísticos de los procesos del punto anterior.

• Finalmente, utilizamos nuestro modelo estimado para

• análisis de escenarios: ¿qué pasaría con la serie de tiempo si recibe una perturbación estocástica de cierta magnitud (función impulso respuesta)

• pronósticos: ¿qué valores esperamos ver en el futuro para esta serie de tiempo?

Modelos que estudiaremos

Ruido blanco

Es una secuencia \(\left\{\epsilon_t\right\}\) cuyos elementos satisfacen,

\[\begin{align*} \E\left(\epsilon_t\right) &=0\\ \E\left(\epsilon^2_t\right) &= \sigma^2 \\ \E\left(\epsilon_t\epsilon_\tau\right) &= 0 \quad\text{for }t\neq\tau \end{align*}\]

Proceso media móvil

Sea \(\left\{\epsilon_t\right\}\) ruido blanco; el proceso estocástico

\[\begin{equation*} y_t = \epsilon_t + \theta_1\epsilon_{t-1} + \dots + \theta_q\epsilon_{t-q} \end{equation*}\]

con \(\theta_q \neq 0\) es llamado un proceso MA(q).

Proceso autorregresivo

Sea \(\left\{\epsilon_t\right\}\) ruido blanco; el proceso estocástico

\[\begin{equation*} y_t = \phi_1y_{t-1} + \dots + \phi_py_{t-p} + \epsilon_t \end{equation*}\]

con \(\phi_p \neq 0\) es llamado un proceso AR(p).

Autorregresivo media móvil

Sea \(\left\{\epsilon_t\right\}\) ruido blanco; el proceso estocástico

\[\begin{multline*} y_t = \phi_1y_{t-1} + \dots + \phi_py_{t-p} + \dots\\ +\epsilon_t + \theta_1\epsilon_{t-1} + \dots + \theta_q\epsilon_{t-q} \end{multline*}\]

es llamado proceso ARMA(p,q).

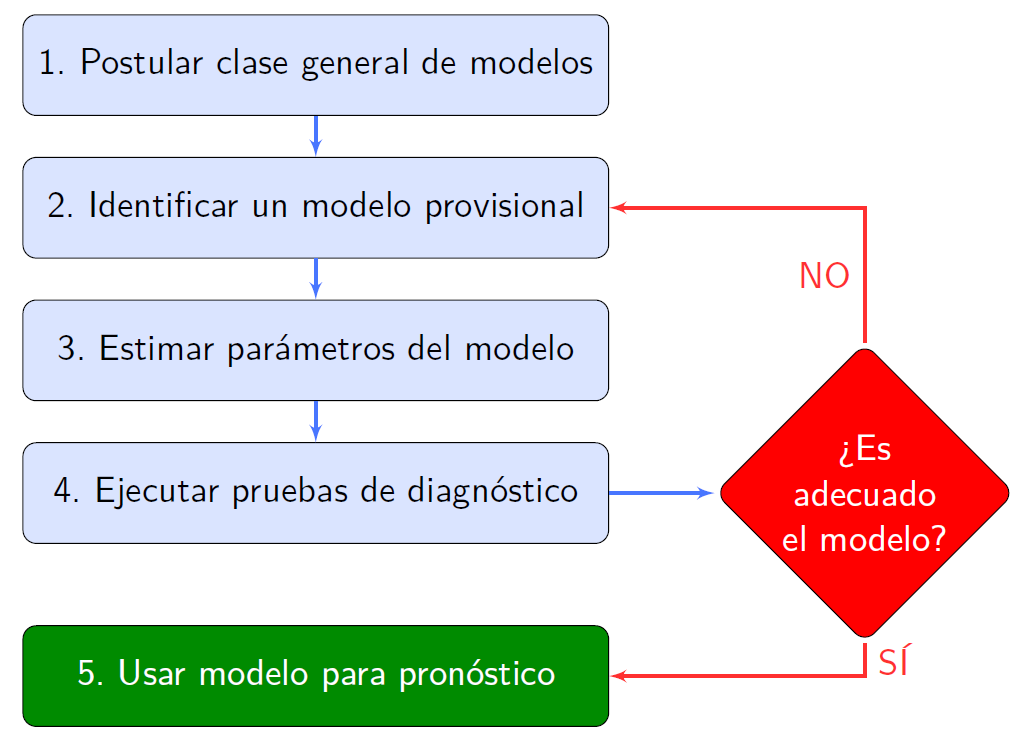
La metodología Box-Jenkins

Acerca de los ejemplos

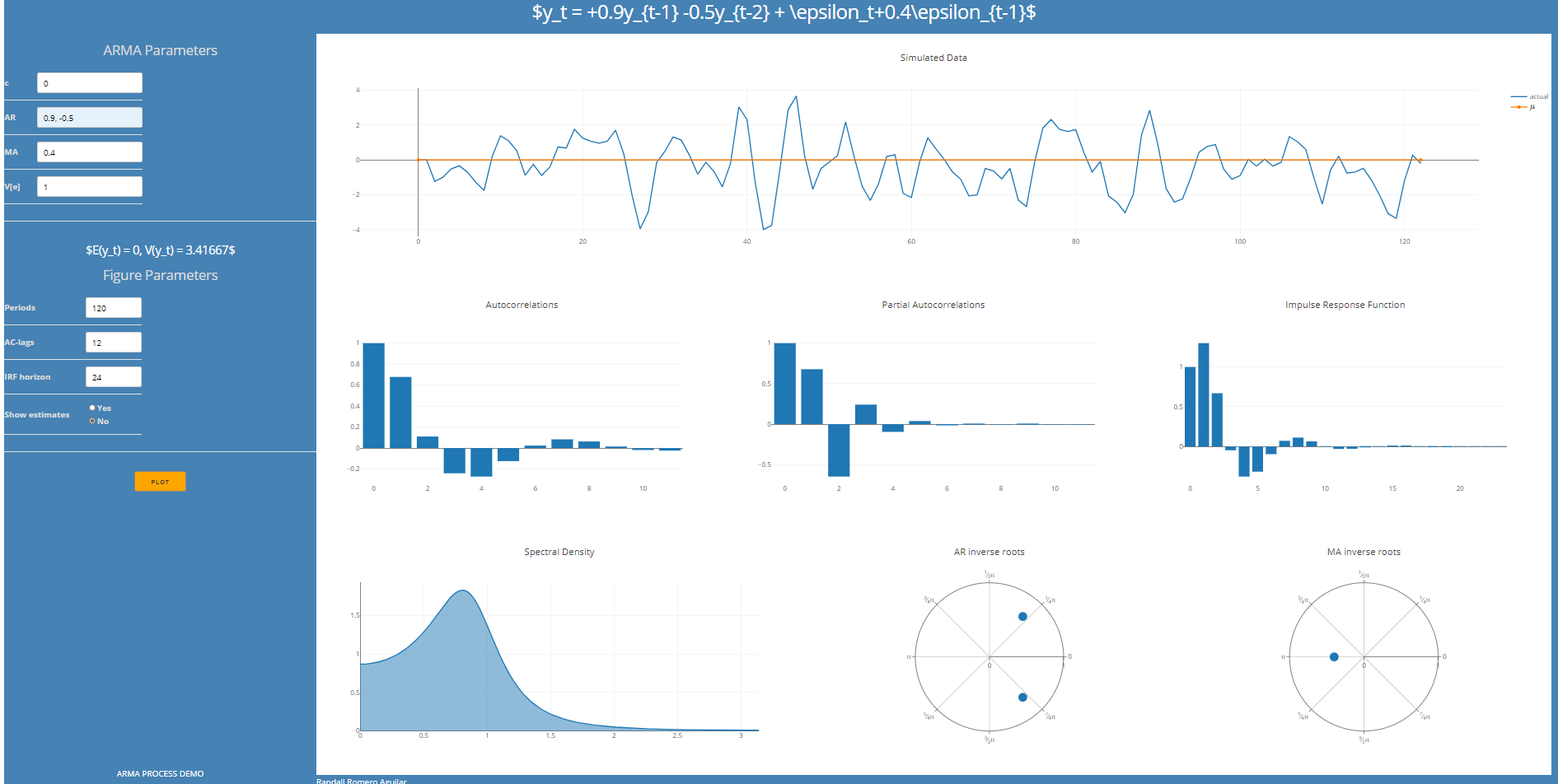
En esta clase veremos ilustraciones de distintos proceso AR, MA, y ARMA.

Usted puede reproducirlas (y estudiar más casos específicos de estos procesos) con el paquete macrodemos que escribí en Python para este tema.

Para instalarlo, en una ventana de sistema:

pip install macrodemos

Para ejecutarlo:

from macrodemos import ARMA_demo
ARMA_demo()