9.2. Valores críticos de MacKinnon para test de cointegración

import numpy as np
import pandas as pd

pd.set_option('precision',5)

GITHUB_REPO = "https://raw.githubusercontent.com/randall-romero/econometria/master/data/"
DATAPATH = GITHUB_REPO if 'google.colab' in str(get_ipython()) else '../data/'

Necesitamos importar una clase de un módulo local. Para ello, usualmente es suficiente con tener el módulo (archivo py) en la misma carpeta que este cuaderno, pero eso no funcionaría cuando se corre en Colab. Por ello, añadimos explícitamente la carpeta que contiene ese módulo en el path de Python.

import sys
sys.path.insert(1, DATAPATH)

Una clase para el test de MacKinnon

from mackinnon import MacKinnon  # este módulo contiene herramientas para calcular valores críticos de MacKinnon
mk = MacKinnon()

El valor crítico al 5% para determinar si 5 series están cointegradas, basados en 100 observaciones, incluyendo intercepto y tendencia lineal

mk('ct', N=5, T=100, level='5%')

nan

Si no especificamos el nivel de significancia, la función muestra los valores usuales de 1%, 5% y 10%

mk('ct', N=5, T=100)

Level
1%    NaN
5%    NaN
10%   NaN
dtype: float64

Para obtener los coeficientes del polinomio de approximación, usamos get_matrix

mk.get_matrix('ct', N=5)

	beta3	beta2	beta1	beta_inf
Level
1%	NaN	50.65	-59.63	0.00012
5%	NaN	91.36	-22.66	0.00007
10%	NaN	76.78	-10.24	0.00005

mk.get_matrix('ct', N=5, level='5%')

beta3            NaN
beta2       91.36000
beta1      -22.66000
beta_inf     0.00007
Name: 5%, dtype: float64

Evaluamos otra vez el valor crítico al 5% para determinar si 5 series están cointegradas, basados en 100 observaciones, incluyendo intercepto y tendencia lineal, esta vez evaluando el polinomio a partir de los coeficientes

b3,b2,b1,b0 = mk.get_matrix('ct', N=5, level='5%')
T = 100
b0 + b1 / T + b2 / T**2 + b3 / T**3

nan

Igual que en el caso anterior, pero usando la función polyval de numpy para evaluar el polinomio

tb = mk.get_matrix('ct', N=5, level='5%')
np.polyval(tb, 1/T)

nan

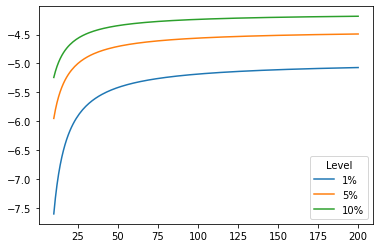
Valores críticos versus tamaño de muestra

Para muestras pequeñas, los valores críticos son mayores (en valor absoluto)

sample_sizes = np.arange(10, 201)
vT = pd.DataFrame([MacKinnon()('c',5,T) for T in sample_sizes], 
                 index=sample_sizes)
vT.plot()

<AxesSubplot:>

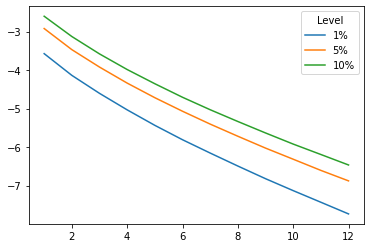
Valores críticos versus número de series

Entre más series hayan en el vector de cointegración, los valores críticos son mayores (en valor absoluto)

number_of_series = np.arange(1, 13)
vN = pd.DataFrame([MacKinnon()('c',N,48) for N in number_of_series], 
                 index=number_of_series)
vN.plot()

<AxesSubplot:>

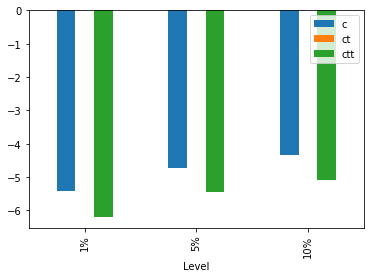
Valores críticos versus tendencias determinísticas

Entre más elementos haya en la tendencia determinística, mayores serán los valores críticos (en valor absoluto)

variants = ['c','ct', 'ctt']
vV = pd.DataFrame([MacKinnon()(v,5,48) for v in variants], 
                 index=variants)
vV.T.plot(kind='bar')

<AxesSubplot:xlabel='Level'>