4.6. Series integradas

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import statsmodels.api as sm

plt.style.use('seaborn')
plt.rc('figure', figsize=(15,4))
plt.rc('axes', titlesize=20, labelsize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=14)
plt.rc('ytick', labelsize=14)
plt.rc('savefig', bbox='tight')

figpath = "../figures/"

Simulaciones de caminatas aleatorias

plt.style.use('seaborn-dark')
pd.options.plotting.backend = "matplotlib"

np.random.seed(2021)

T = 60 # horizonte
n = 100 # cantidad de simulaciones

𝜖 = pd.DataFrame(np.random.randn(T+1, n)) # ruido blanco
y = 𝜖.cumsum(axis=0)  # caminatas aleatorias


fig = plt.figure(figsize=(14, 8))
gs = fig.add_gridspec(5, 2,  width_ratios=(6, 2),
                      left=0.1, right=0.9, bottom=0.1, top=0.9,
                      wspace=0.05, hspace=0.05)

# -----------Graficar las simulaciones
ax = fig.add_subplot(gs[:, 0])
y.plot(color='RoyalBlue', alpha=0.1, legend=False, ax=ax)
ax.axhline(0, color='white');
ax.set(title=f'{n} caminatas aleatorias',ylim=[-25,25])

# -----------Histogramas
ax_last = None
for i in range(5):
    ax_last = fig.add_subplot(gs[i, 1], sharex= ax_last)
    y.loc[15*i].hist(ax=ax_last, color='RoyalBlue', alpha=0.8)
    if i==0:
        ax_last.set(title='Histogramas',xlim=[-25,25])

    ax_last.set_yticks([])
    ax_last.annotate(f't ={15*i}', (0.1, 0.8), xycoords='axes fraction')
    
fig.savefig(figpath + 'Simulaciones-caminata-aleatoria.pdf')    

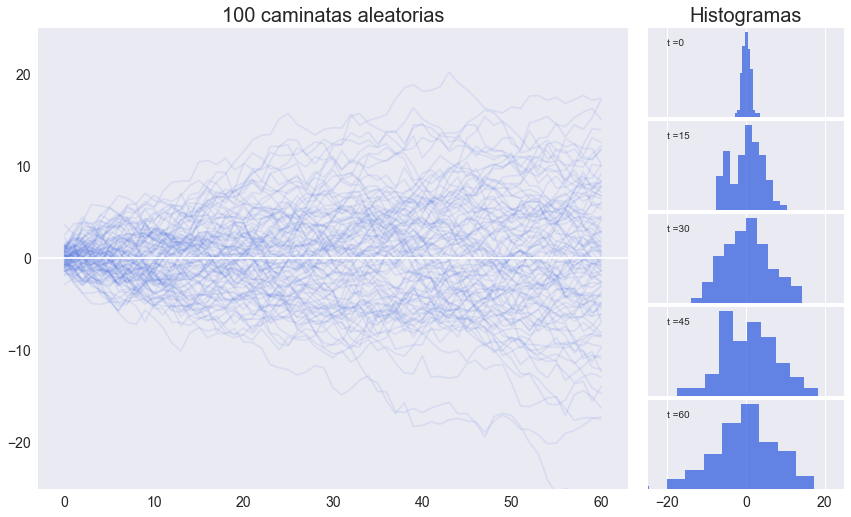
Simulaciones de caminatas aleatorias con deriva

pd.options.plotting.backend = "matplotlib"
a = 0.5 # deriva
y = (𝜖+a).cumsum(axis=0)  # caminatas aleatorias con deriva


fig = plt.figure(figsize=(14, 8))
gs = fig.add_gridspec(5, 2,  width_ratios=(6, 2),
                      left=0.1, right=0.9, bottom=0.1, top=0.9,
                      wspace=0.05, hspace=0.05)

ax = fig.add_subplot(gs[:, 0])
y.plot(color='RoyalBlue', alpha=0.1, legend=False, ax=ax)
ax.plot(a*np.arange(T), color='white');
ax.set(title=f'{n} caminatas aleatorias con deriva',ylim=[-10,50])

ax_last = None
for i in range(5):
    ax_last = fig.add_subplot(gs[i, 1], sharex= ax_last)
    y.loc[15*i].hist(ax=ax_last, color='RoyalBlue', alpha=0.8)
    if i==0:
        ax_last.set(title='Histogramas',xlim=[-10,50])

    ax_last.set_yticks([])
    ax_last.annotate(f't ={15*i}', (0.05, 0.8), xycoords='axes fraction')
    
fig.savefig(figpath + 'Simulaciones-caminata-aleatoria-con-deriva.pdf')        

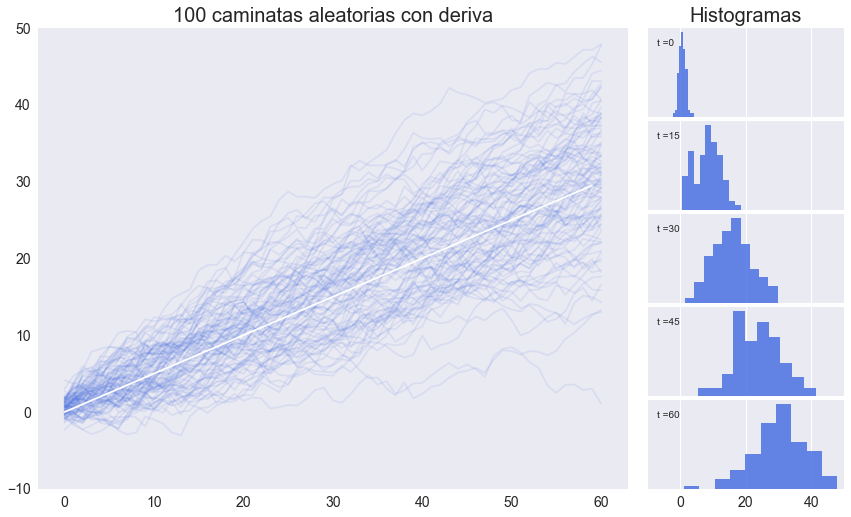
Autocorrelación de una caminata aleatoria

def rw_rho(t, smax=20):
    """
    Calcula las primera autocorrelaciones de una serie con raiz unitaria
    
    Ver pagina 56 de los apuntes del tema 4 del curso
    """
    return np.sqrt(1 - np.arange(smax+1) /t)

rw_rho_data = pd.DataFrame({f't={t}':rw_rho(t) for t in [20,40,60,80]})
     
fig, ax = plt.subplots()
rw_rho_data.plot(ax=ax)
ax.set(ylim=[0,1], xticks=np.arange(0,21,4), xlabel='rezagos', title='Autocorrelaciones')
plt.savefig(figpath + 'rw-rho.pdf', bbox_inches='tight')

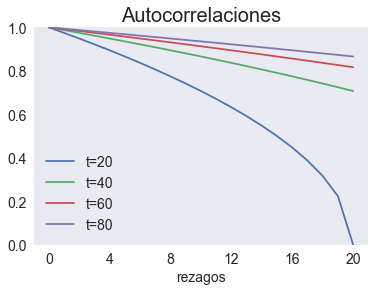
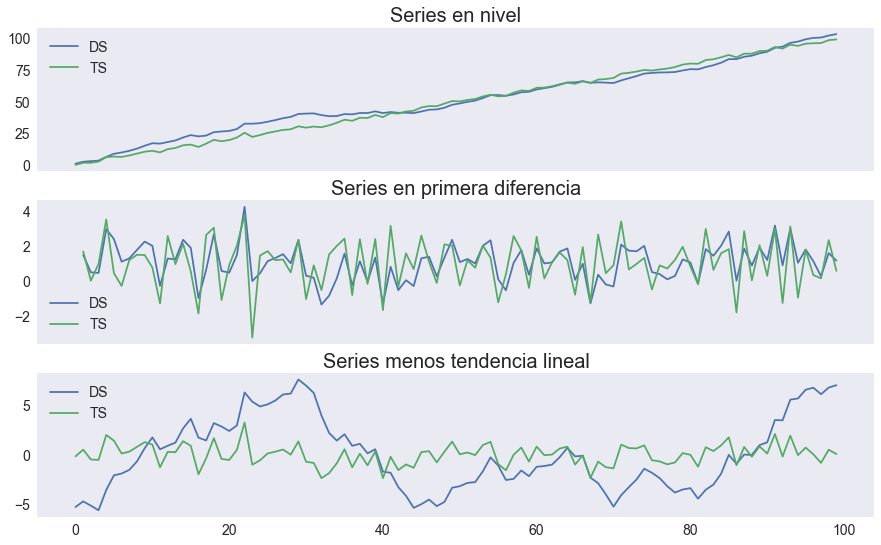
Estacionario en diferencia vs estacionario en tendencia

Ejemplo basado en Levendis 2019, pp. 109-113. Muestra que no es tan fácil distinguir a simple vista un proceso estacionario en diferencia de uno estacionario alrededor de una tendencia.

T = 100
np.random.seed(12345)
tt = np.arange(T)
e = np.random.randn(T)

datos = pd.DataFrame({'t':tt, 'e':e}, index=tt)
datos['DS'] = (1+e).cumsum()
datos['TS'] = 1*tt + e
datos

	t	e	DS	TS
0	0	-0.204708	0.795292	-0.204708
1	1	0.478943	2.274236	1.478943
2	2	-0.519439	2.754797	1.480561
3	3	-0.555730	3.199067	2.444270
4	4	1.965781	6.164847	5.965781
...	...	...	...	...
95	95	0.795253	99.254214	95.795253
96	96	0.118110	100.372324	96.118110
97	97	-0.748532	100.623793	96.251468
98	98	0.584970	102.208762	98.584970
99	99	0.152677	103.361439	99.152677

100 rows × 4 columns

%%timeit
lento = pd.DataFrame({'t':tt, 'e':e}, index=tt)

# caminata aleatoria
y = np.zeros(T)
y[0] = 1 + e[0]
for t in range(1, T):
    y[t] = 1 + y[t-1] + e[t]

# estacionario alrededor de tendencia    
x = np.zeros(T)
x[0] = e[0]
for t in range(1, T):
    x[t] = 1 * tt[t] + e[t]

lento['y'] = y
lento['x'] = x
#lento

2.27 ms ± 373 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

detrended = pd.DataFrame(
    {'DS':smf.ols('DS ~ t', datos).fit().resid,
     'TS':smf.ols('TS ~ t', datos).fit().resid
    }, index=tt)

def ols_ala_stata(formula):
    return smf.ols(formula, datos).fit().summary()

ols_ala_stata('DS ~ t + TS -1')

OLS Regression Results

Dep. Variable:	DS	R-squared (uncentered):	0.993
Model:	OLS	Adj. R-squared (uncentered):	0.993
Method:	Least Squares	F-statistic:	7233.
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	3.71e-107
Time:	00:12:21	Log-Likelihood:	-297.34
No. Observations:	100	AIC:	598.7
Df Residuals:	98	BIC:	603.9
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
t	0.4261	0.463	0.921	0.359	-0.492	1.344
TS	0.5768	0.462	1.248	0.215	-0.340	1.494

Omnibus:	17.306	Durbin-Watson:	0.027
Prob(Omnibus):	0.000	Jarque-Bera (JB):	6.610
Skew:	0.374	Prob(JB):	0.0367
Kurtosis:	1.986	Cond. No.	111.

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

fig, axs = plt.subplots(3,1, figsize=[15,9], sharex=True)
series = ['DS', 'TS']
datos[series].plot(ax=axs[0], title='Series en nivel')
datos[series].diff().plot(ax=axs[1], title='Series en primera diferencia')
detrended[series].plot(ax=axs[2], title='Series menos tendencia lineal')

<AxesSubplot:title={'center':'Series menos tendencia lineal'}>

np.random.seed(1)
T = 121
e = np.random.randn(T)
e[0] = 0

x0 = y0 = a = 1
t = np.arange(T)

y = y0 + a*t + e.cumsum()
x = x0 + a*t + e

ejemplo = pd.DataFrame({'DS':y,'TS':x})    

fig, ax = plt.subplots()
ejemplo.plot(ax=ax)
ax.set_title('Tendencia determinística (TS) versus estocástica (DS)', fontsize=16)
fig.suptitle('Series no estacionarias',fontsize=24, y=1.05)
fig.savefig(figpath + 'TS-DS-sample.pdf')

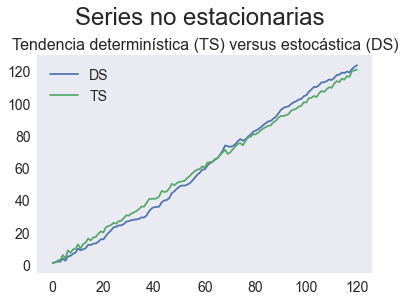
Repetimos el ejercicio, pero con un millón de observaciones

T = 1_000_000
np.random.seed(12345)
tt = np.arange(T)
e = np.random.randn(T)

big = pd.DataFrame({'t':tt, 'e':e}, index=tt)
big['DS'] = (1+e).cumsum()
big['TS'] = tt + e

bigdetrended = pd.DataFrame(
    {'DS':smf.ols('DS~t', big).fit().resid,
     'TS':smf.ols('TS~t', big).fit().resid
    }, index=tt)

resumen = pd.concat([
    big[series].diff().describe().T,
    bigdetrended[series].describe().T
], keys=['1-diff', '- tend'])

resumen

		count	mean	std	min	25%	50%	75%	max
1-diff	DS	999999.0	1.001494e+00	0.999954	-4.057590	0.326730	1.001364	1.674426	5.979780
	TS	999999.0	1.000001e+00	1.414065	-5.800262	0.046267	1.000069	1.951536	7.517358
- tend	DS	1000000.0	-3.559082e-09	158.846292	-405.803718	-118.686166	-15.663626	136.408845	372.938439
	TS	1000000.0	6.236537e-10	0.999953	-5.058701	-0.674670	-0.000123	0.672972	4.978591