4.1. Replicando el trabajo de Dickey y Fuller#

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from scipy.stats import t as t_Student

plt.style.use('seaborn')
plt.rc('figure', figsize=(15,4))
plt.rc('axes', titlesize=20, labelsize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=14)
plt.rc('ytick', labelsize=14)

Distribución de Dickey-Fuller#

La siguiente función genera una muestra aleatoria de T datos, estima tres regresiones (todas ellas la serie contra su primer rezago, difieren en los términos estocásticos) y retorna los respectivos estadísticos t estimados.

def df_simulacion(T=101):
    e = np.random.randn(T)
    y = e.cumsum()
    dy = y[1:]-y[:-1]
    X = sm.add_constant(y[:-1])
    Z = np.c_[X,np.arange(T-1)]
    
    res0 = sm.OLS(dy, y[:-1], hasconst=False).fit()
    res1 = sm.OLS(dy, X, hasconst=True).fit()
    res2 = sm.OLS(dy, Z, hasconst=True).fit()
    return res0.tvalues[0], res1.tvalues[1], res2.tvalues[1]

Por ejemplo, esta simulación da estos tres valores del estadístico t: uno solo la serie rezagada, el segundo agrega un intercepto, y el tercero un intercepto y una tendencia determinística.

df_simulacion()

(-2.333795703754419, -2.437920571284451, -2.392897993146313)

Simulando los estadísticos (secuencialmente)#

Simulemos una muestra de 100 mil observaciones.

N = 100_000

%%time
dfvalues = pd.DataFrame([df_simulacion() for _ in range(N)], columns=['nc','c','ct'])

CPU times: total: 3min 28s
Wall time: 3min 29s

Simulando los estadíticos (en paralelo)#

Vemos que tarda bastante tiempo (cerca de 2 minutos en mi PC). La mayoría de los computadores modernos contienen un procesador de varios núcleos, por lo que podríamos ejecutar esta simulación más rápidamente si utilizamos todos los núcleos disponibles (aprovechando que todas las realizaciones de nuestra simulación deben ser independientes). Para ello definimos la función Monte_Carlo

from joblib import Parallel, delayed

def Monte_Carlo(funcion, repeticiones, columnas, *args, **kwargs):
    """
    Ejecuta simulaciones de Montecarlo en paralelo, aprovechando todos los núcleos del procesador

    Argumentos:
        funcion: una función que dé por resultado una única realización de las cantidades que se desean simular
        repeticiones: un entero que indica cuántas muestras se desean simular
        columnas: una lista (o tupla) de strings, que identifiquen a las cantidades individuales retornadas por funcion
        *args, **kwargs: otros parámetros requeridos por funcion

    Retorna:
         Un data frame de pandas, con tantas filas como `repeticiones` y columnas como textos en `columnas`.
    """
    datos = Parallel(n_jobs=-1)(delayed(funcion)(*args, **kwargs) for _ in range(repeticiones))
    return pd.DataFrame(datos, columns=columnas)

%%time
dfvalues = Monte_Carlo(df_simulacion, N, ['nc','c','ct'])

CPU times: total: 42.7 s
Wall time: 1min 55s

En mi PC, que contiene un procesador de 4 núcleos, el tiempo se redujo de 2 minutos a solo 33 segundos (el tiempo exacto cambia de una ejecución a otra). En adelante, seguiremos utilizando la función Monte_Carlo para hacer las simulaciones en paralelo.

Graficando la distribución de Dickey-Fuller#

def plot_df(ax, data, titulo,df):
    maxtval = 5.0
    t5crit = t_Student.isf(0.05, df)

    ff, edges = np.histogram(data, bins=100, density=True)
    center = (edges[1:] + edges[:-1])/2
    w = center[1] - center[0]

    ax.bar(center, ff, width=w, alpha=0.5)
    xvals = np.linspace(-4,4, 200)
    ax.plot(xvals, t_Student.pdf(xvals, df=99), '-r')
    ax.set(xlim=[-maxtval, maxtval], title=titulo)
    ax.legend(['t-student', 'simulada'], loc='upper left')

    # valores críticos
    df5 = data.quantile(0.05)
    ax.axvline(-t5crit, ls="--", color='red')
    ax.axvline(df5, ls="--", color='gray')

    # error tipo I
    err1 = (data < -t5crit).mean()*100
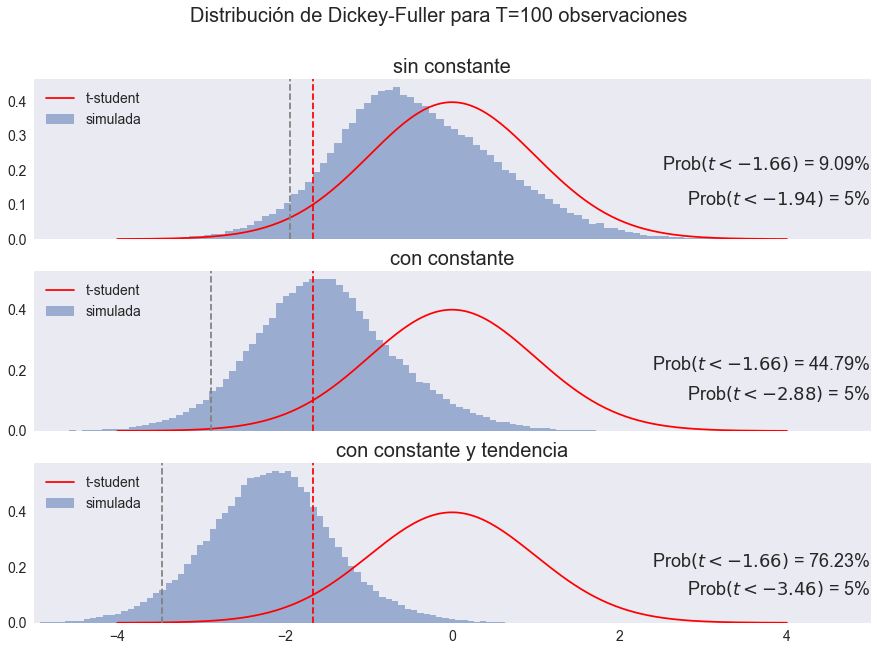
    ax.annotate(f'Prob$\\left(t < -1.66\\right)$ = {err1:.2f}%', (5,0.2), size=18, ha='right')
    ax.annotate(f'Prob$\\left(t < {df5:.2f}\\right)$ = 5%', (5,0.1), size=18, ha='right')
    ax.grid(False)


fig, (ax0, ax1, ax2) = plt.subplots(3,1, figsize=[15,10], sharex=True)

plot_df(ax0, dfvalues['nc'],'sin constante',99)
plot_df(ax1, dfvalues['c'],'con constante',98)
plot_df(ax2, dfvalues['ct'],'con constante y tendencia',97)

fig.suptitle('Distribución de Dickey-Fuller para T=100 observaciones', size=20)
fig.savefig('Dickey-Fuller.pdf', bbox_inches='tight')

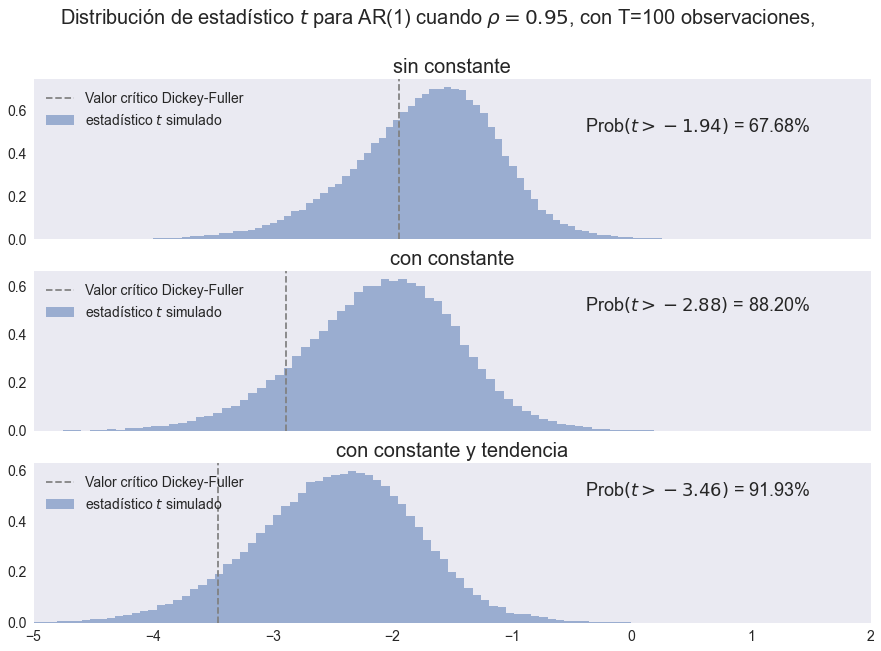
Potencia de la prueba#

df5crit = dfvalues.quantile(0.05)
df5crit

nc   -1.941314
c    -2.884849
ct   -3.461125
Name: 0.05, dtype: float64

def df_simulacion_power(rho=0.95, T=101):
    e = np.random.randn(T)
    y = np.zeros(T)
    for t in range(1,T):
        y[t] = rho*y[t-1] + e[t]
    
    dy = y[1:] -y[:-1]
    X = sm.add_constant(y[:-1])
    Z = np.c_[X,np.arange(T-1)]
    
    res0 = sm.OLS(dy, y[:-1], hasconst=False).fit()
    res1 = sm.OLS(dy, X, hasconst=True).fit()
    res2 = sm.OLS(dy, Z, hasconst=True).fit()
    return res0.tvalues[0], res1.tvalues[1], res2.tvalues[1]

df_simulacion_power()

(-2.19743316126669, -2.187957698002359, -3.086619842452488)

%%time
dfvaluespower = Monte_Carlo(df_simulacion_power, N, columnas=['nc','c','ct'])

CPU times: total: 1min 23s
Wall time: 2min 6s

def plot_df2(ax, data, spec, titulo,df):
    #maxtval = 5.0
    #t5crit = t.isf(0.05, df)

    ff, edges = np.histogram(data, bins=100, density=True)
    center = (edges[1:] + edges[:-1])/2
    w = center[1] - center[0]

    ax.bar(center, ff, width=w, alpha=0.5)
    #xvals = np.linspace(-4,4, 200)
    #ax.plot(xvals, t.pdf(xvals, df=99), '-r')
    ax.set(xlim=[-5, 2], title=titulo)
    

    # valores críticos
    df5 = df5crit[spec]
    ax.axvline(df5, ls="--", color='gray')
    ax.legend(['Valor crítico Dickey-Fuller', 'estadístico $t$ simulado'], loc='upper left')
    # error tipo II
    
    err2 = (data > df5).mean()*100
    ax.annotate(f'Prob$\\left(t > {df5:.2f}\\right)$ = {err2:.2f}%', (1.5,0.5), size=18, ha='right')
    ax.grid(False)

fig, (ax0, ax1, ax2) = plt.subplots(3,1, figsize=[15,10], sharex=True)

plot_df2(ax0, dfvaluespower['nc'],'nc','sin constante',99)
plot_df2(ax1, dfvaluespower['c'],'c','con constante',98)
plot_df2(ax2, dfvaluespower['ct'],'ct','con constante y tendencia',97)

fig.suptitle('Distribución de estadístico $t$ para AR(1) cuando $\\rho=0.95$, con T=100 observaciones, ', size=20)
fig.savefig('Dickey-Fuller-power.pdf', bbox_inches='tight')

Apuntes de Macroeconometría

Replicando el trabajo de Dickey y Fuller

Contents