1.2. Autocorrelograma y pruebas de ruido blanco para el IMAE de Costa Rica#

Ejemplo numérico para ilustrar el uso del autocorrelograma y el autocorrelograma parcial.

Nota Para ejecutar este cuaderno se requiere el paquete bccr. Si no lo tiene, ejecute la siguiente celda

try:
    import bccr
except ImportError:
    print('Module bccr missing. Installing it now')
    !pip install bccr

from bccr import SW
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats.distributions import chi2
import os

figpath = "../figures/"

Importamos los datos#

La clase ServicioWeb permite obtener datos directamente del Banco Central de Costa Rica

Buscamos series que tenga “IMAE” en su DESCRIPCION, frecuencia mensual. Filtramos los resultados para ver solo las series en nivel, y dejamos solo aquellos qe tengan la palabra “IMAE” en su descripción

imaes = SW.buscar(todos='IMAE', frecuencia='M')
imaes = imaes[imaes.Unidad == 'Nivel']
imaes[imaes.descripcion.str.contains('IMAE')]
DESCRIPCION descripcion Unidad Medida periodo
codigo
913 Node('/BCCR/Sector Real/IMAE con IEAT, Serie Original [913]') Indice Mensual de Actividad Económica (IMAE) con la Industria Electronica de Alta Tecnologia (IEAT). Serie Original Nivel NO DEFINIDO Mensual
914 Node('/BCCR/Sector Real/IMAE con IEAT, Tendencia Ciclo [914]') Índice Mensual de Actividad Económica (IMAE) con la Industria Electrónica de Alta Tecnología (IEAT). Serie Tendencia... Nivel NO DEFINIDO Mensual
915 Node('/BCCR/Sector Real/IMAE sin IEAT, Serie Original [915]') Índice Mensual de Actividad Económica (IMAE) sin la Industria Electrónica de Alta Tecnología (IEAT). Serie Original Nivel NO DEFINIDO Mensual
916 Node('/BCCR/Sector Real/IMAE sin IEAT, Tendencia Ciclo [916]') Índice Mensual de Actividad Económica (IMAE) sin la Industria Electrónica de Alta Tecnología (IEAT). Serie Tendencia... Nivel NO DEFINIDO Mensual
22718 Node('/BCCR/Sector Real/IMAE con IEAT, Desestacionalizada [22718]') Índice Mensual de Actividad Económica (IMAE) con la Industria Electrónica de Alta Tecnología (IEAT). Serie Desestaci... Nivel NO DEFINIDO Mensual
25158 Node('/BCCR/Sector Real/IMAE con IEAT, Desestacionalizada [22718]/IMAE específico [25158]') IMAE específico1991=100 Nivel No definida Mensual
22967 Node('/BCCR/Sector Real/IMAE sin Zona Franca Serie Original [22967]') IMAE sin Zona Franca Serie Original Nivel NO DEFINIDO Mensual
22970 Node('/BCCR/Sector Real/IMAE sin Zona Franca Serie Tendencia Ciclo [22970]') IMAE sin Zona Franca Serie Original Nivel NO DEFINIDO Mensual
35449 Node('/BCCR/Sector Real/IMAE , Serie Original [35449]') IMAE , Serie Original Nivel NO DEFINIDO Mensual
35553 Node('/BCCR/Sector Real/IMAE Tendencia Ciclo [35553]') IMAE Tendencia Ciclo Nivel NO DEFINIDO Mensual
35660 Node('/BCCR/Sector Real/IMAE, Serie Desestacionalizadal [35660]') IMAE, Serie Desestacionalizadal Nivel NO DEFINIDO Mensual

De esta lista, escogemos los indicadores 35449 (serie original) y 35553 (tendencia-ciclo) (éstas están discontinuadas, usarememos entonces las series 87703 y 87764, que de momentos no pueden encontrarse con bccr, pero sí descargarse). Descargamos los datos y cambiamos los nombres de las series.

imae = SW(Original=87703, Tendencia_ciclo=87764)

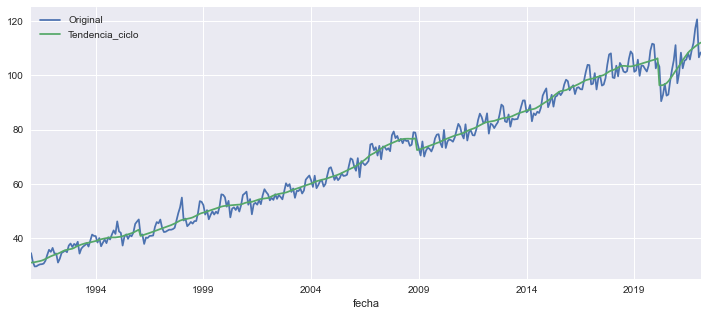
Graficamos las dos series para ver su dinamica.

imae.plot(figsize=[12,5])

<AxesSubplot:xlabel='fecha'>
../_images/correlogram_9_1.png

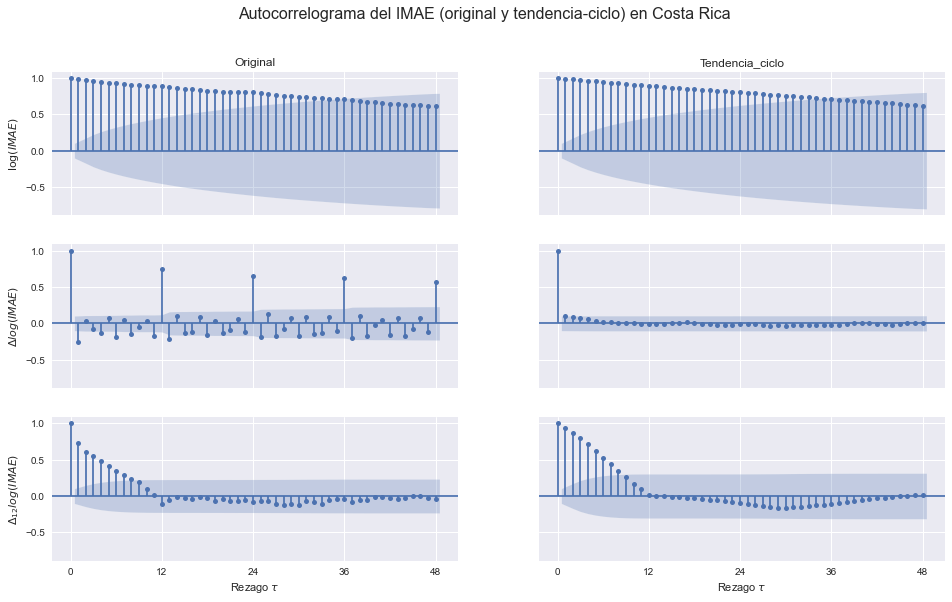
Autocorrelograma#

Obtenemos autocorrelogramas (48 rezagos, con intervalos de 95% de significancia (Bartlett)) para las series en nivel, primera diferencia, y diferencia estacional.

OPCIONES = dict(lags=48, alpha=0.05, title='')
plot_acf = sm.graphics.tsa.plot_acf
plot_pacf = sm.graphics.tsa.plot_pacf
log_imae = np.log(imae)

fig, axs = plt.subplots(3,2, figsize=[16,9], sharex=True, sharey=True)

for indic, ax in zip(imae, axs.T):
    plot_acf(log_imae[indic].dropna(), ax=ax[0], **OPCIONES);
    plot_acf(log_imae[indic].diff().dropna(), ax=ax[1], **OPCIONES);
    plot_acf(log_imae[indic].diff(12).dropna(), ax=ax[2], **OPCIONES);

for indic, ax in zip(imae, axs[0]):
    ax.set_title(indic)

for ax in axs[-1]:
    ax.set_xlabel(r'Rezago $\tau$')
    ax.set_xticks(np.arange(0,49,12));

axs[0,0].set_ylabel(r'$\log(IMAE)$')
axs[1,0].set_ylabel(r'$\Delta log(IMAE)$')
axs[2,0].set_ylabel(r'$\Delta_{12} log(IMAE)$')

fig.suptitle('Autocorrelograma del IMAE (original y tendencia-ciclo) en Costa Rica', size=16)
fig.savefig(figpath + 'IMAE-acf.pdf', bbox_inches='tight')
../_images/correlogram_12_0.png

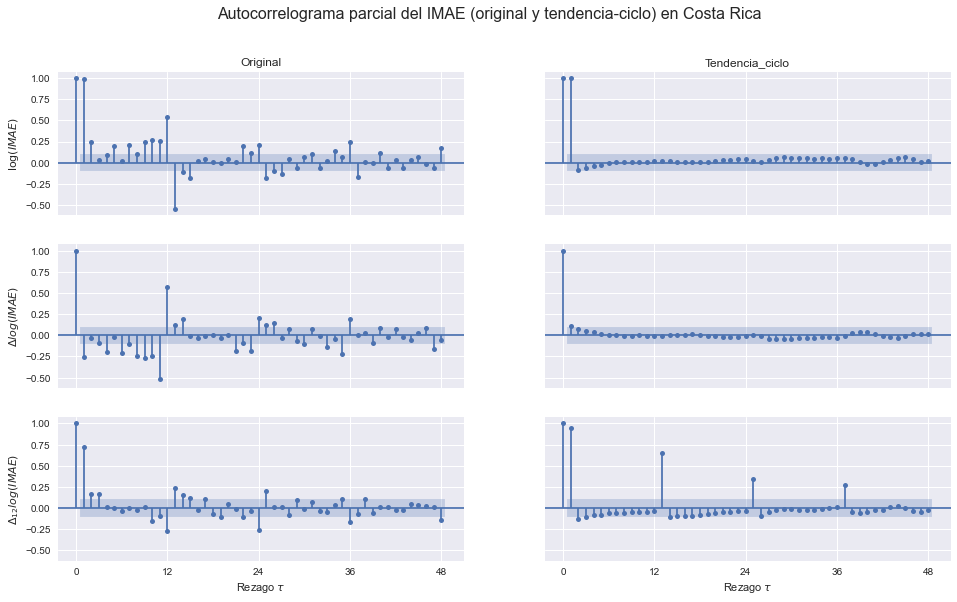
Autocorrelograma parcial#

Repetimos el ejercicio, pero esta vez obtenemos autocorrelogramas parciales (48 rezagos, con intervalos de 95% de significancia) para las series en nivel, primera diferencia, y diferencia estacional.

OPCIONES = dict(lags=48, alpha=0.05, title='', method='ols')

fig, axs = plt.subplots(3,2, figsize=[16,9], sharex=True, sharey=True)

for indic, ax in zip(imae, axs.T):
    plot_pacf(log_imae[indic].dropna(), ax=ax[0], **OPCIONES);
    plot_pacf(log_imae[indic].diff().dropna(), ax=ax[1], **OPCIONES);
    plot_pacf(log_imae[indic].diff(12).dropna(), ax=ax[2], **OPCIONES);

for indic, ax in zip(imae, axs[0]):
    ax.set_title(indic)

for ax in axs[-1]:
    ax.set_xlabel(r'Rezago $\tau$')
    ax.set_xticks(np.arange(0,49,12));

axs[0,0].set_ylabel(r'$\log(IMAE)$')
axs[1,0].set_ylabel(r'$\Delta log(IMAE)$')
axs[2,0].set_ylabel(r'$\Delta_{12} log(IMAE)$')

fig.suptitle('Autocorrelograma parcial del IMAE (original y tendencia-ciclo) en Costa Rica', size=16)
fig.savefig(figpath + 'IMAE-pacf.pdf', bbox_inches='tight')
../_images/correlogram_14_0.png

Pruebas de ruido blanco#

¿Es es crecimiento mensual del IMAE tendencia-ciclo un proceso ruido blanco?

growth = log_imae['Tendencia_ciclo'].diff().dropna()
T = growth.size  # número de datos
M = 7   # máximo número de rezagos
rezagos = np.arange(1, M+1)
alpha = 0.05  # significancia de los test

Calculamos las autocovarianzas, a partir de un rezago

rho = sm.tsa.acf(growth, fft=True, nlags=M)[1:]

Calculamos el estadístico de Box-Pierce, para todos los rezagos desde el 1 hasta el 7

(1.1)#\[\begin{equation} Q^{*} = T\sum_{j=1}^{m}\hat{\rho}_j^2 \; \overset{\text{asy}}{\sim} \; \chi^2_{m-k} \end{equation}\]
Qstar = T * (rho ** 2).cumsum()

Calculamos el estadístico de Ljung-Box

(1.2)#\[\begin{equation} Q = T(T+2)\sum_{j=1}^{m}\frac{\hat{\rho}_j^2}{T-j} \; \overset{\text{asy}}{\sim} \; \chi^2_{m-k} \end{equation}\]
Q = T * (T+2) * ((rho ** 2)/(T-rezagos)).cumsum()

Calculamos los valores críticos, tomando en cuenta que \(k=0\) porque los datos que estamos usando no son residuos

vcrits = np.array([chi2(k).ppf(1-alpha) for k in rezagos])

Con carácter informativo nada más, calculamos la autocorrelación parcial

rhop = sm.tsa.pacf(growth, nlags=M, method='ols')[1:]

Juntamos todos los resultados en una tabla de resumen.

resumen = pd.DataFrame({'AC':rho, 'PAC': rhop, 'Box-Pierce':Qstar, 'Ljung-Box':Q, f'$\chi^2(m-k)$': vcrits}, index=rezagos)
resumen.index.name = 'Rezagos'

resumen.round(3)
AC PAC Box-Pierce Ljung-Box $\chi^2(m-k)$
Rezagos
1 0.106 0.106 4.184 4.218 3.841
2 0.085 0.075 6.885 6.948 5.991
3 0.068 0.052 8.596 8.682 7.815
4 0.057 0.040 9.790 9.896 9.488
5 0.034 0.017 10.231 10.345 11.070
6 0.021 0.006 10.402 10.520 12.592
7 0.016 0.005 10.499 10.619 14.067

Exportar datos#

Finalmente, exportamos los datos para poder replicar este ejercicio con otros programas (Stata, EViews, R).

log_imae.to_csv('log_imae.csv')