\[ \begin{align}\begin{aligned}\require{color} \newcommand{\alert}[1]{{\color{RedOrange} #1}} \newcommand{\notation}[2]{\underset{\color{MidnightBlue}\text{#2}}{#1}} \newcommand{\simbolo}[2]{\underset{\color{MidnightBlue}#2}{#1}} \newcommand{\notationbrace}[2]{{\underbrace{#1}_{\color{MidnightBlue}\text{#2}}}} \DeclareMathOperator{\dd}{\,d\!} \DeclareMathOperator{\E}{\mathbb{E}{}} \DeclareMathOperator{\Var}{Var{}} \DeclareMathOperator{\Cov}{Cov{}} \DeclareMathOperator{\Lag}{L{}} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator{\Prob}{\mathbb{P}} \newcommand{\marginal}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\MAT}[1]{\begin{bmatrix} #1 \end{bmatrix}} \newcommand{\mat}[1]{\left[\begin{smallmatrix} #1 \end{smallmatrix}\right]}\\\begin{split}\DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\X}{\mathbf{x}} \DeclareMathOperator{\y}{\mathbf{y}} \DeclareMathOperator{\h}{\mathbf{h}} \newcommand{\stackEq}[1]{\MAT{#1_1 \\ #1_2 \\ \vdots \\ #1_M}} \newcommand{\e}{\mathbf{\epsilon}} \newcommand{\Y}{\mathbf{Y}} \newcommand{\estimator}[2]{{\hat{#1}^{\text{#2}}}} \newcommand{\estimate}[2]{\underset{(#2)}{#1}} \DeclareMathOperator{\plim}{plim} \newcommand{\PLIM}[2]{#1\xrightarrow{p} #2}\end{split}\end{aligned}\end{align} \]

3.1. Introducción#

¿Qué es una serie de tiempo?#

Una serie de tiempo \(\{y_t\}_{t=1}^T\) es una realización de un proceso estocástico.

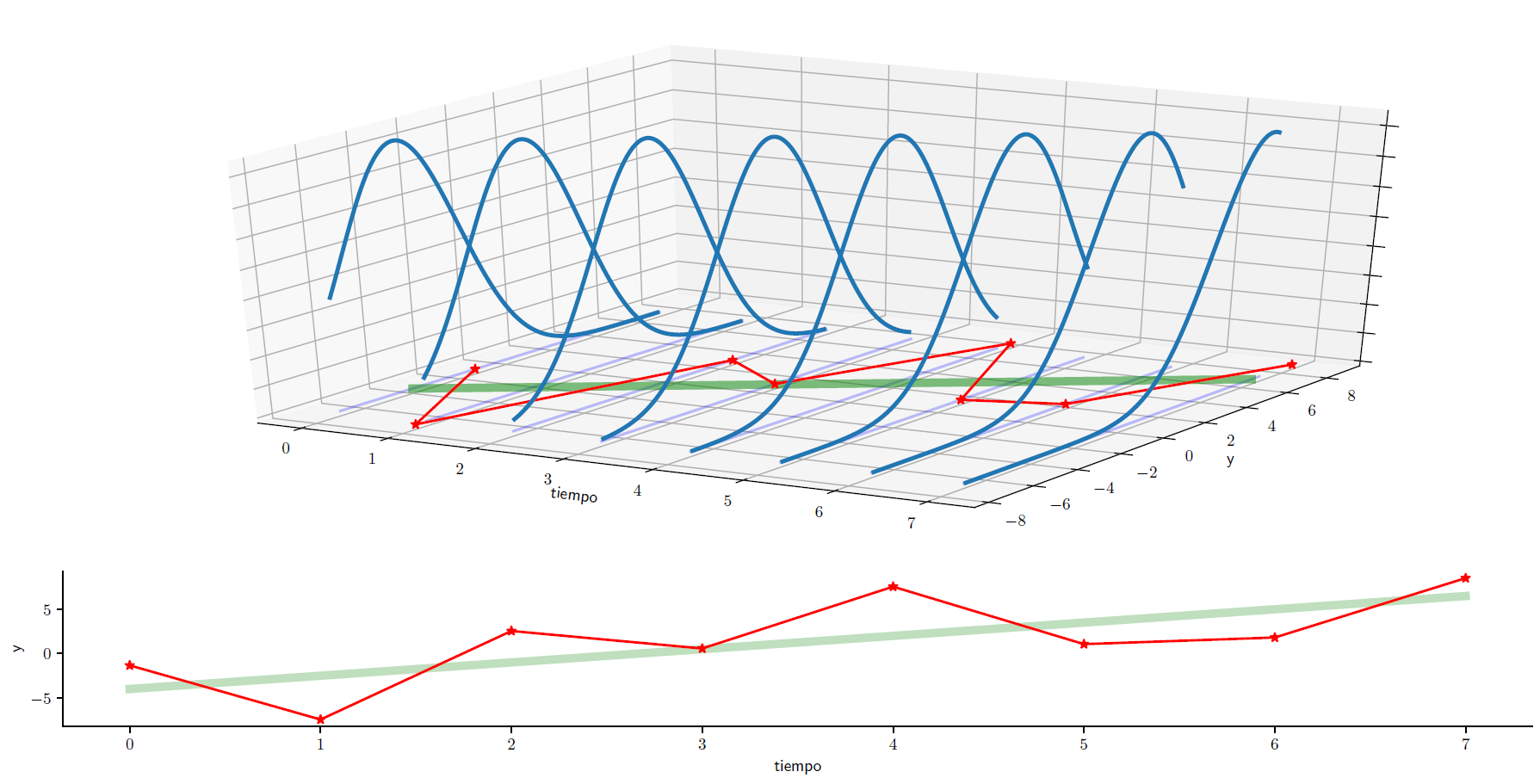
../../_images/serie-no-estacionaria1.png

¿Qué nos gustaría hacer con esta serie de tiempo?#

Imaginemos a la serie de tiempo como la parte de un proceso estocástico para la cual ya tenemos las realizaciones del proceso (un valor por período)

\[\begin{equation*} \notationbrace{y_1, y_2,\dots,y_T}{datos observados},\notationbrace{y_{T+1}, y_{T+2},\dots}{futuro} \end{equation*}\]

Nos gustaría saber la distribución condicional

\[\begin{equation*} \Prob\left[y_{T+j} \leq x\;|\;y_1,\dots, y_T\right] \end{equation*}\]

Esto nos permitiría utilizar nuestra serie de tiempo para pronosticar valores futuros de la serie, así como precisar su variabilidad:

\[\begin{align*} \E_T\left[y_{T+j}\right] &\equiv \E\left[y_{T+j}\;|\;y_1\dots, y_T\right] \\ \Var_T\left[y_{T+j}\right] &\equiv \Var\left[y_{T+j}\;|\;y_1,\dots, y_T\right] \end{align*}\]

Nuestra tarea#

En la práctica, puede ser que nunca conozcamos el verdadero proceso generador de datos (PGD) (el proceso estocástico del cual fueron obtenidos los valores de nuestra serie de tiempo).

Nuestra tarea es desarrollar modelos que capturen la esencia del verdadero PGD.

Las ecuaciones en diferencia estocásticas son una manera muy conveniente de modelar procesos económicos dinámicos.

Ejemplo:   Controlando la oferta de dinero

Suponga que la meta de oferta monetaria \(M^*\) del banco central crece 100g% por año:

\[\begin{equation*} M_t^* = (1+g)M_{t-1}^* \end{equation*}\]

o en términos logarítmicos, con \(m^*\equiv \log\left(M^*\right)\)

\[\begin{align*} m_t^* &= \log(1+g) + m_{t-1}^* \\ &\approx g + m_{t-1}^* \end{align*}\]

Para una condición inicial \(m_0^*\) dada, la solución es:

\[\begin{equation*} m_t^* = gt + m_{0}^* \end{equation*}\]

La cantidad efectiva de dinero \(m_t\) puede diferir de la meta \(m_t^*\).

El banco central intenta cerrar una proporción \(\rho\) de la brecha entre la meta y la cantidad efectiva del período anterior. El cambio en la oferta de dinero es:

\[\begin{equation*} \Delta m_t = \notation{\rho\left(m_{t-1}^* - m_{t-1}\right)}{política monetaria} + \notation{\epsilon_t}{perturbación} \end{equation*}\]

por lo que la oferta de dinero es

\[\begin{align*} m_t &= \rho m_{t-1}^* + (1-\rho)m_{t-1} + \epsilon_t \\ &= \rho g(t-1) + \rho m_{0}^* + (1-\rho)m_{t-1} + \epsilon_t \\ &= \notationbrace{\rho(m_{0}^* - g)}{intercepto} + \notationbrace{(\rho g) t}{tendencia} + \notationbrace{(1-\rho)m_{t-1}}{autorregresivo} + \notationbrace{\epsilon_t}{shock} \end{align*}\]

Aunque la oferta monetaria es una variable continua, nuestro modelo es una ecuación en diferencia (discreta).

Como las perturbaciones \(\left\{\epsilon_t\right\}\) son aleatorias, la oferta de dinero es estocástica.

Si supiéramos la distribución de \(\left\{\epsilon_t\right\}\), podríamos calcular la distribución de cada elemento de \(\left\{m_t\right\}\), porque está determinada completamente por los parámetros de la ecuación y por la secuencia \(\left\{\epsilon_t\right\}\).

Habiendo observado las primeras \(T\) observaciones de la serie \(\left\{m_t\right\}\), podríamos pronosticar futuros valores. Por ejemplo:

\[\begin{align*} m_{T+1} &= \rho\left(gT + m_{0}^*\right) + (1-\rho)m_{T} + \epsilon_{T+1} \\ \Rightarrow \E_T\left[m_{T+1}\right] &= \rho\left(gT + m_{0}^*\right) + (1-\rho)m_{T} \end{align*}\]

Ruido blanco y el modelo clásico de regresión lineal#

En el MCRL se asume que

\[\begin{equation*} y_t = x'_t\beta + \epsilon_t \end{equation*}\]

donde para todas las observaciones \(t=1,2,\dots,T\) el término de error cumple que:

\[\begin{align*} \E[\epsilon_t] &=0 \tag{media cero} \\ \Var[\epsilon_t] &=\sigma^2 \tag{no hay heteroscedasticidad} \\ \E[\epsilon_t\epsilon_\tau] &=0 \quad\text{si } t\neq\tau \tag{no hay autocorrelación} \end{align*}\]

Es decir, el MCRL aplicado a series de tiempo asume que el error es un proceso de ruido blanco.

Sin embargo, en la práctica rara vez se satisface ese supuesto cuando se ajusta un modelo de regresión lineal a datos de series de tiempo.

Ejemplo:   Estimando la demanda de dinero

Consideremos la demanda de dinero en Costa Rica

\[\begin{equation*} \log(M_t) = \beta_0 + \beta_1\log(q_t) + \beta_2\log(p_t) + \beta_3\log(i_t) + \epsilon_t \end{equation*}\]

la cual estimamos con datos mensuales (1991m01 a 2020m01) del medio circulante \(M_t\), el IMAE \(q_t\), el IPC \(p_t\), y la tasa básica pasiva \(i_t\).

import bccr
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import matplotlib.gridspec as gridspec

import statsmodels.api as sm
from statsmodels.formula.api import ols


datos = bccr.SW(IMAE=35449, IPC=25482, M1=1445, Tbasica=423, func=np.mean, fillna='ffill').dropna()
datos.tail()
IMAE IPC M1 Tbasica
fecha
2020-07 110.987099 106.127077 5.166828e+06 3.708065
2020-08 110.584336 106.122788 5.206881e+06 3.635484
2020-09 113.705524 106.411930 5.206211e+06 3.498333
2020-10 118.613059 106.496597 5.061595e+06 3.293548
2020-11 120.969090 106.498184 4.913216e+06 3.346667 
res = ols('M1 ~ IMAE + IPC + Tbasica', data=np.log(datos)).fit()
res.summary()
OLS Regression Results
Dep. Variable: M1 R-squared: 0.994
Model: OLS Adj. R-squared: 0.994
Method: Least Squares F-statistic: 1.944e+04
Date: Thu, 21 Jul 2022 Prob (F-statistic): 0.00
Time: 00:13:54 Log-Likelihood: 335.36
No. Observations: 359 AIC: -662.7
Df Residuals: 355 BIC: -647.2
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 6.3294 0.298 21.263 0.000 5.744 6.915
IMAE 1.0242 0.079 13.044 0.000 0.870 1.179
IPC 0.9268 0.028 33.508 0.000 0.872 0.981
Tbasica -0.3519 0.022 -15.919 0.000 -0.395 -0.308
Omnibus: 115.244 Durbin-Watson: 0.450
Prob(Omnibus): 0.000 Jarque-Bera (JB): 463.868
Skew: 1.349 Prob(JB): 1.87e-101
Kurtosis: 7.872 Cond. No. 390.


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

No obstante, los residuos de la regresión no parecen ruido blanco.

fig = plt.figure(figsize=[10,5], tight_layout=True)
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, :])
axs0 = fig.add_subplot(gs[1,0])
axs1 = fig.add_subplot(gs[1,1], sharey=axs0)

res.resid.plot(title='Residuos de la regresión', ax=ax)

OPCIONES = dict(lags=48, alpha=0.05, )
sm.graphics.tsa.plot_acf(res.resid, ax=axs0, title='Autocorrelación',**OPCIONES);
sm.graphics.tsa.plot_pacf(res.resid, ax=axs1, title='Autocorrelación parcial', **OPCIONES);
axs0.set_xticks([0,12,24,36,48])
axs1.set_xticks([0,12,24,36,48]);
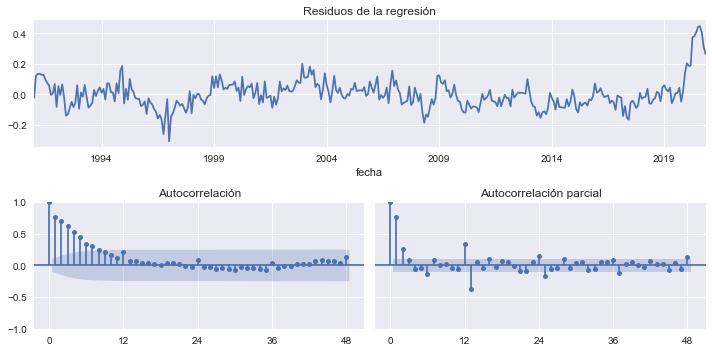
../../_images/01-intro_4_1.png

Conocer el valor de un residuo puede ayudar a pronosticar el siguiente.

Aún así, notemos que para pronosticar el valor del M1 en 2020m12, necesitaríamos pronosticar los valores de las demás variables.