2.1. Resolviendo una ecuación en diferencia con sympy#

Este cuaderno resuelve la ecuación en diferencia

\[\begin{equation*} y_t = 0.9y_{t-1} -0.2y_{t-2} + 3 \end{equation*}\]

que está incluida en el tema “2. Ecuaciones en diferencia”.

import numpy as np
from sympy import Function, rsolve
from sympy.abc import t
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')

y = Function('y')

Solución analítica#

Solución ecuación homogénea#

rsolve(y(t) - 0.9*y(t-1) + 0.2*y(t-2), y(t))
\[\displaystyle 0.4^{t} C_{0} + 0.5^{t} C_{1}\]

Solución general#

rsolve(y(t) - 0.9*y(t-1) + 0.2*y(t-2) - 3, y(t))
\[\displaystyle 0.4^{t} C_{0} + 0.5^{t} C_{1} + 10.0\]

Solución general con condiciones iniciales#

z = rsolve(y(t) - 0.9*y(t-1) + 0.2*y(t-2) - 3, y(t), {y(0):13, y(1): 11.3})
z
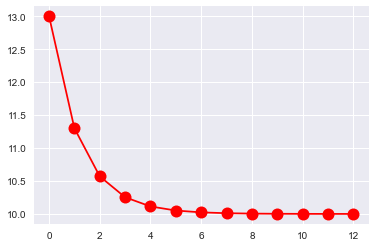
\[\displaystyle 2.0 \cdot 0.4^{t} + 1.0 \cdot 0.5^{t} + 10.0\]
tt = np.arange(13)
plt.plot(tt, 2*0.4**tt+0.5**tt+10, 'ro-', markersize=12)

[<matplotlib.lines.Line2D at 0x2c70f77f7f0>]
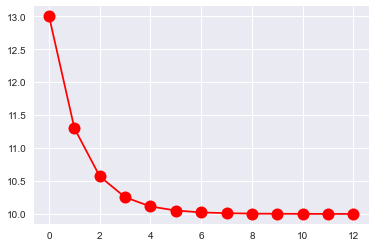
../_images/EqDiff2_10_1.png

Solución recursiva a partir de condiciones iniciales#

T = 13
Y = np.zeros(T)
Y[:2] = 13, 11.3


for t in range(2, T):
    Y[t] = 0.9*Y[t-1]-0.2*Y[t-2] + 3

plt.plot(Y,'ro-', markersize=12)

[<matplotlib.lines.Line2D at 0x2c710861760>]
../_images/EqDiff2_12_1.png