1.5. Series de tiempo#

Definición de serie de tiempo#

Una serie de tiempo es una colección de observaciones indexadas por la fecha de cada observación, denotada por \(y_t\)

\[\begin{equation*} y_1, y_2, \dots, y_T \end{equation*}\]

En la práctica se asume que lo anterior es sólo una muestra, pero que la serie pudo haber sido observada en más períodos.

\[\begin{equation*} \dots, y_{-1}, y_0, \alert{y_1, y_2, \dots, y_T}, y_{T+1}, y_{T+2}, \dots \end{equation*}\]

Así, vemos a una serie de tiempo como una realización del proceso estocástico \(\{Y_t\}^\infty_{t=-\infty}\), de la cual solo tenemos observaciones para \(t\) entre 1 y \(T\).

Serie de tiempo estacionaria#

Una serie de tiempo estacionaria es una realización de un proceso estocástico estacionario.

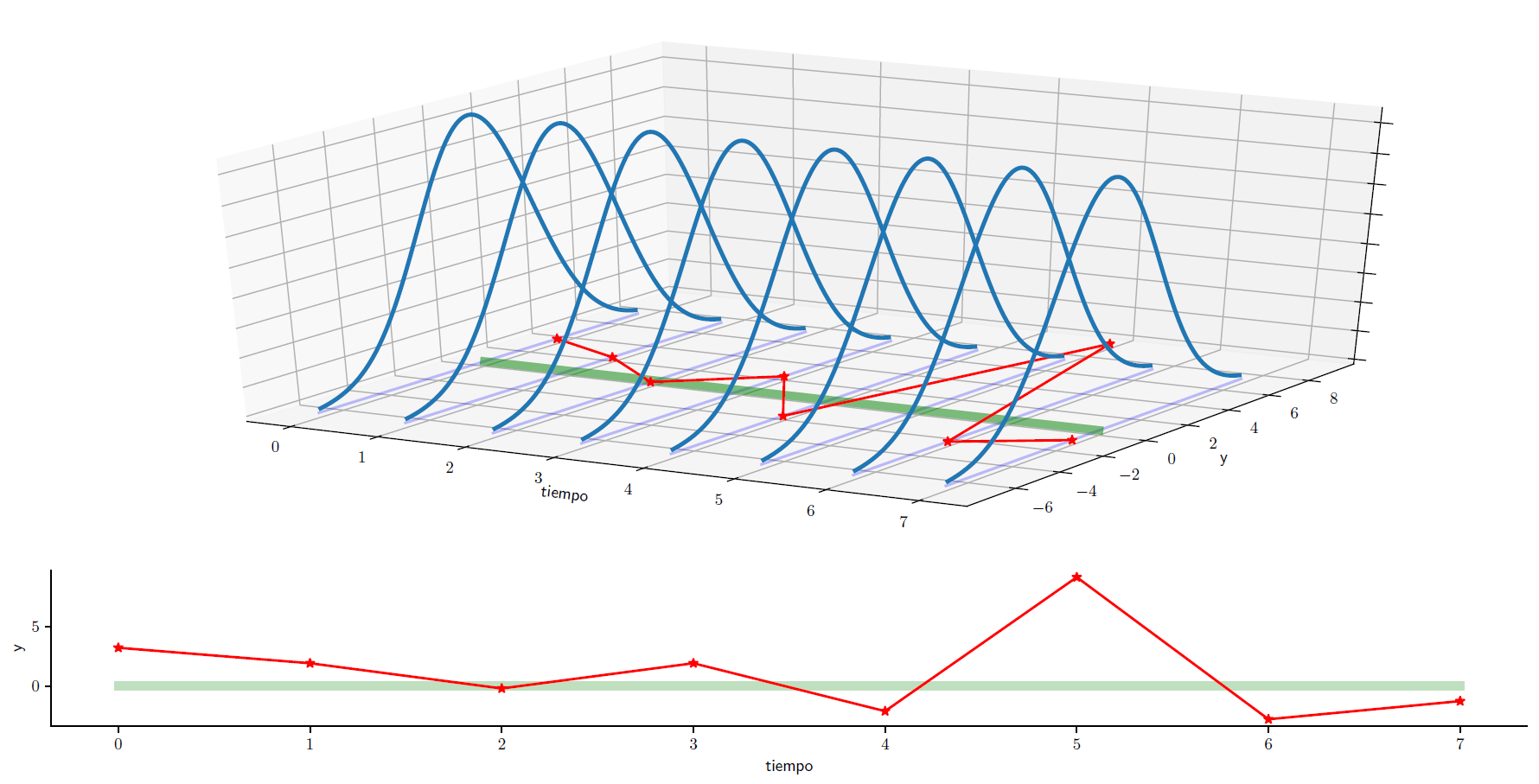
Fig. 1.5 Una serie estacionaria#

Serie de tiempo no estacionaria#

Una serie de tiempo no estacionaria es una realización de un proceso estocástico no estacionario.

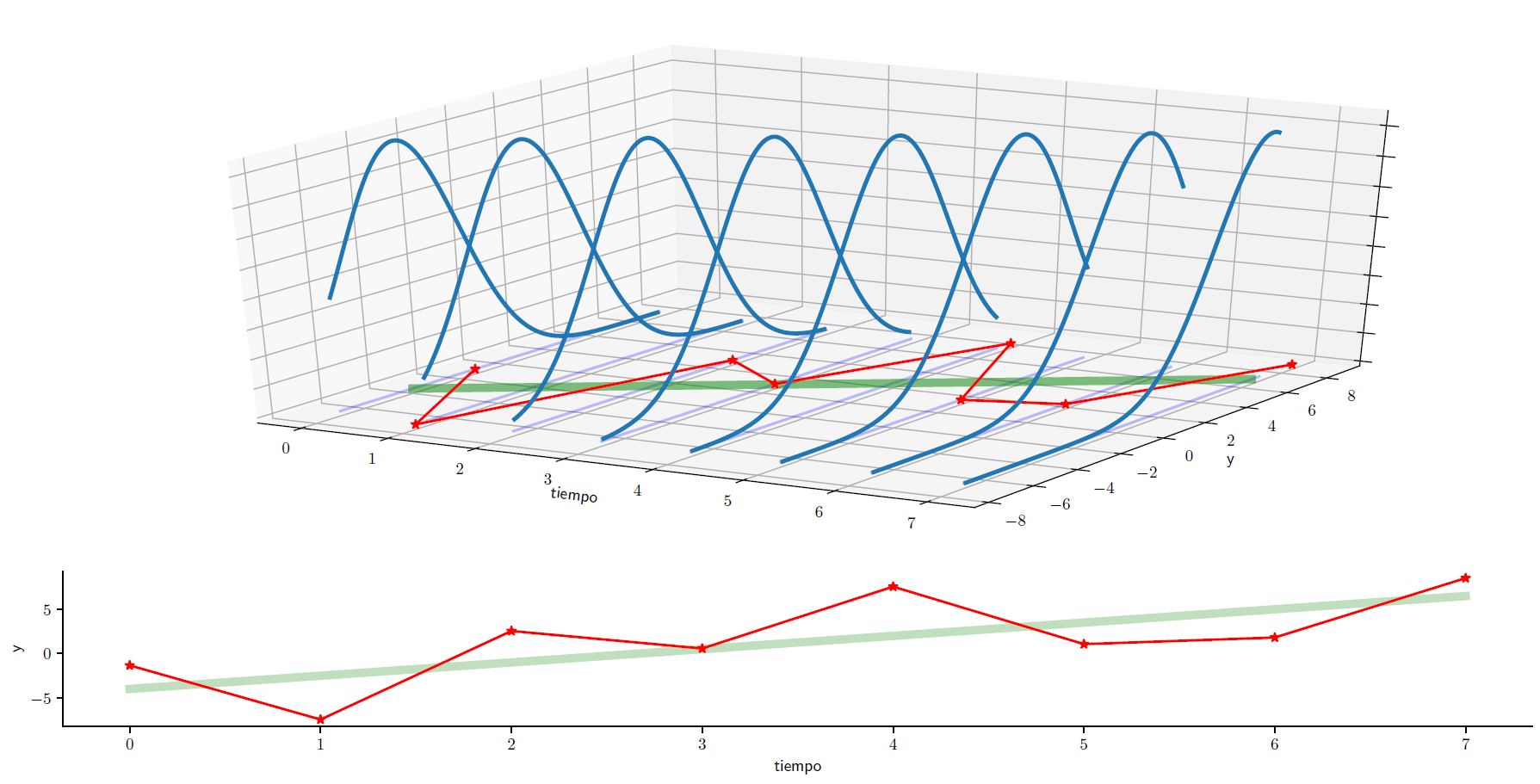
Fig. 1.6 Una serie no estacionaria#

Casos particulares de series de tiempo#

Tendencia

\[\begin{equation*} y_t = t \end{equation*}\]

Constante

\[\begin{equation*} y_t = c \end{equation*}\]

Ruido blanco de Gauss

\[\begin{equation*} y_t = \epsilon_t, \text{ con } \left(\epsilon_t\right)_{t=-\infty}^{\infty} i.i.d., \epsilon_t\sim N(0,\sigma^2) \end{equation*}\]

Infiriendo los momentos del proceso estocástico#

Suponga que tenemos un número grande \(n\) de realizaciones independientes del proceso estocástico \(\{Y_t\}^T_{t=1}\), y que deseamos estimar el valor del momento no central \(\mu'_{k,t} \equiv \E[Y^k_t]\). Utilizando la ley de los grandes números, podemos estimarlo así

\[\begin{equation*} \hat{\mu'}_{k,t} = \frac{y^k_{t,1} + y^k_{t,2} + \dots y^k_{t,n}}{n} \end{equation*}\]

En la práctica, sólo tenemos una única realización del proceso: \(y_1, y_2, \dots, y_T\).

¿Podemos estimar \(\mu'_{k,t}\) a partir de \(\overline{y^k} = \frac{y^k_{1} + y^k_{2} + \dots y^k_{T}}{T}\)? En general no, a menos que el proceso estocástico sea

estacionario
ergódico (para el momento \(k\)).

Ergodicidad#

En el caso de procesos estacionarios, el supuesto de ergodicidad significa que momentos muestrales calculados a partir de una serie de tiempo con un número finito de observaciones converge (en algún sentido) a sus contrapartes poblacionales.

Ergódico en media

El proceso es ergódico en media si

\[\begin{equation*} \lim\limits_{T\to\infty}\E\left[\left(\tfrac{1}{T}\sum_{t=1}^{T}y_t - \mu \right)^2\right] = 0 \end{equation*}\]

Ergódico en varianza

El proceso es ergódico en varianza si

\[\begin{equation*} \lim\limits_{T\to\infty}\E\left[\left(\tfrac{1}{T}\sum_{t=1}^{T}(y_t - \mu)^2 - \sigma^2_y \right)^2\right] = 0 \end{equation*}\]

Algunas apuntes acerca de la ergodicidad#

Las condiciones de ergodicidad son “propiedades de consistencia” para variables aleatorias dependientes, y no pueden ser evaluadas. Por ello, deben ser asumidas.
No podemos usar la ley de los grandes números para probar ergodicidad, porque las distribuciones de distintos momentos \(t\) pueden ser idénticas, pero en general no son independientes.
Un proceso no estacionario no puede ser ergódico: ¿a los momentos de cuál variable \(Y_t\) convergerían los momentos muestrales si los poblacionales no fueran constantes?

Estimación de momentos de un proceso estacionario#

Si el proceso es ergódico, podemos estimar consistentemente:

Media

\[\begin{equation*} \hat{\mu} = \frac{1}{T}\sum\limits_{t=1}^{T}y_t \end{equation*}\]

Varianza

\[\begin{equation*} \hat{\gamma}_0 = \frac{1}{T}\sum\limits_{t=1}^{T}(y_t - \hat{\mu})^2 \end{equation*}\]

Autocovarianza

\[\begin{equation*} \hat{\gamma}_\tau = \frac{1}{T}\sum\limits_{t=1}^{T-\tau}(y_t - \hat{\mu})(y_{t+\tau} - \hat{\mu}) \end{equation*}\]

Autocorrelación

\[\begin{equation*} \hat{\rho}_\tau = \frac{\hat{\gamma}_\tau}{\hat{\gamma}_0} \quad \text{para } \tau = 1, 2,\dots T-1. \end{equation*}\]

Asimetría

\[\begin{equation*} \hat{S} = \frac{\frac{1}{T}\sum\limits_{t=1}^{T}(y_t - \hat{\mu})^3}{\sqrt{\hat{\gamma}_0^3}} \end{equation*}\]

Kurtosis

\[\begin{equation*} \hat{K} = \frac{\frac{1}{T}\sum\limits_{t=1}^{T}(y_t - \hat{\mu})^4}{\hat{\gamma}_0^2} \end{equation*}\]

Autocorrelación#

Es imposible evaluar qué tan fuerte es la dependencia de variables de un proceso estocástico a partir de las autocovarianzas, porque éstas dependen de las unidades de medida de la serie. Por ello, utilizamos las autocorrelaciones, que se obtienen de dividir las autocovarinzas por la varianza del proceso.

Si el proceso es estacionario se cumple que:

\(\rho_0 = 1\)
\(\rho_\tau = \rho_{-\tau}\)
\(\left|\rho_\tau\right|\leq 1\) para todo \(\tau\).

LLamamos autocorrelograma a la secuencia de autocorrelaciones \(\rho_\tau\), vista como función del número de rezagos \(\tau\).

Autocorrelación muestral#

En la práctica, a partir de una muestra estimaremos la autocorrelación muestral.

Como nuestra muestra es finita, los valores estimados no necesariamente coincidirán con los poblacionales. Por ello, nos interesa especialmente saber cuándo estas autocorrelaciones son significativamente distintas de cero. Según Bartlett (1946), la varianza de los coeficientes de autocorrelación en los cuales \(\rho_{k+1}, \rho_{k+2}, \dots = 0\) está dada por

\[\begin{equation*} V\left[\hat{\rho}(\tau)\right] \approx \frac{1}{T}\left(1+2\sum_{j=1}^k\rho(j)^2\right) \end{equation*}\]

Autocorrelación parcial#

La \(m\)-ésima autocorrelación parcial \(\hat{a}_m^{(m)}\) se estima por OLS como el último coeficiente de una regresión de \(y\) en una constante y sus \(m\) valores más recientes:

\[\begin{equation*} y_t = c + \hat{a}_1^{(m)}y_{t-1} + \hat{a}_2^{(m)}y_{t-2} + \dots + \hat{a}_m^{(m)}y_{t-m} +\hat{\epsilon_{t+1}} \end{equation*}\]

La idea es medir el efecto directo de, por ejemplo, \(y_{t-1}\) sobre \(y_{t+1}\), controlando por el efecto indirecto que \(y_{t-1}\) pueda tener sobre \(y_{t+1}\) a través de \(y_{t}\).

Si los datos están generados por un proceso AR(p), entonces el estimador \(\hat{a}_m^{(m)}\) tiene una varianza alrededor del verdadero valor (cero) aproximada por

\[\begin{equation*} \Var\left[\hat{a}_m^{(m)}\right] \approx\frac{1}{T} \qquad\text{ para } m = p+1,p+2, \dots \end{equation*}\]

Ejemplo: Autocorrelograma del IMAE

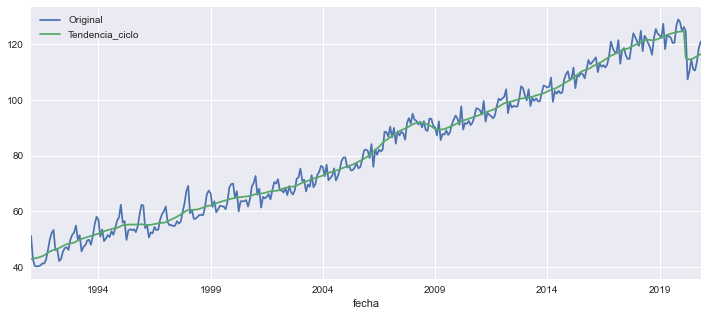
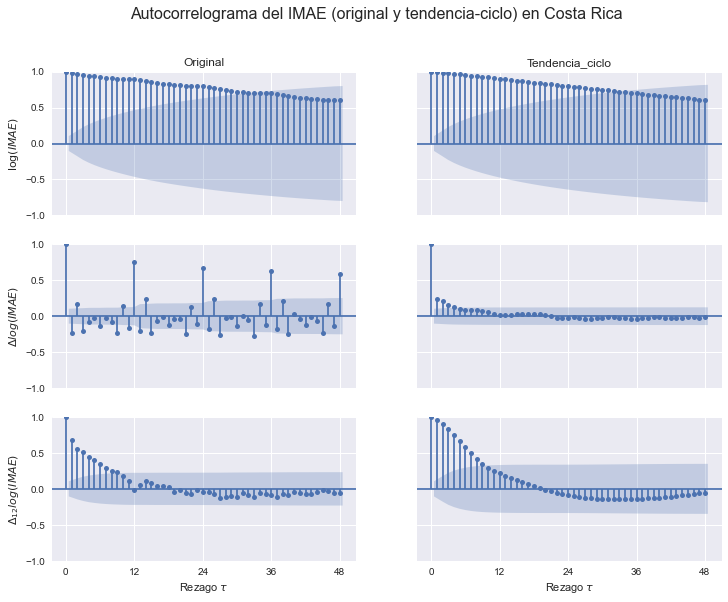
Obtenemos y graficamos los datos

imae = SW(Original=35449, Tendencia_ciclo=35553)
imae.plot(figsize=[12,5]);

plot_acf = sm.graphics.tsa.plot_acf
plot_pacf = sm.graphics.tsa.plot_pacf
log_imae = np.log(imae)

Hacemos los autocorrelogramas

OPCIONES = dict(lags=48, alpha=0.05, title='')

fig, axs = plt.subplots(3,2, figsize=[12,9], sharex=True, sharey=True)

for indic, ax in zip(imae, axs.T):
    plot_acf(log_imae[indic].dropna(), ax=ax[0], **OPCIONES);
    plot_acf(log_imae[indic].diff().dropna(), ax=ax[1], **OPCIONES);
    plot_acf(log_imae[indic].diff(12).dropna(), ax=ax[2], **OPCIONES);

for indic, ax in zip(imae, axs[0]):
    ax.set_title(indic)

for ax in axs[-1]:
    ax.set_xlabel(r'Rezago $\tau$')
    ax.set_xticks(np.arange(0,49,12));

axs[0,0].set_ylabel(r'$\log(IMAE)$')
axs[1,0].set_ylabel(r'$\Delta log(IMAE)$')
axs[2,0].set_ylabel(r'$\Delta_{12} log(IMAE)$')

fig.suptitle('Autocorrelograma del IMAE (original y tendencia-ciclo) en Costa Rica', size=16);

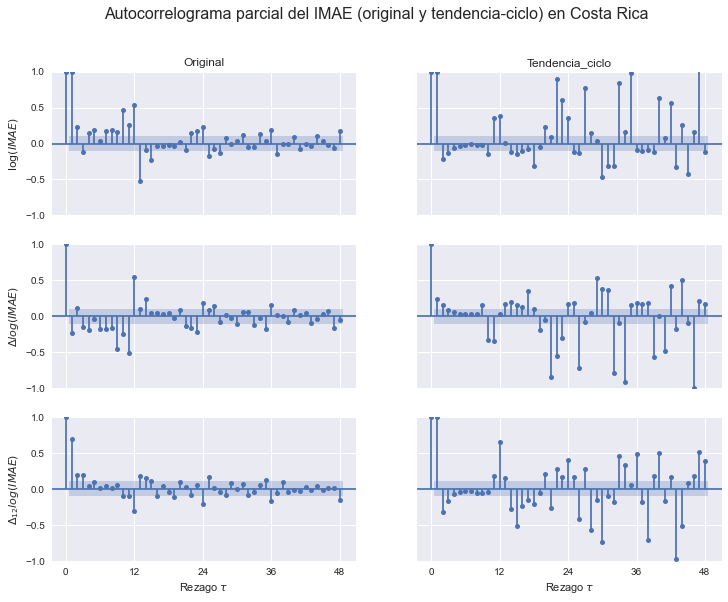
Hacemos los autocorrelogramas parciales

OPCIONES = dict(lags=48, alpha=0.05, title='', method='ols')

fig, axs = plt.subplots(3,2, figsize=[12,9], sharex=True, sharey=True)

for indic, ax in zip(imae, axs.T):
    plot_pacf(log_imae[indic].dropna(), ax=ax[0], **OPCIONES);
    plot_pacf(log_imae[indic].diff().dropna(), ax=ax[1], **OPCIONES);
    plot_pacf(log_imae[indic].diff(12).dropna(), ax=ax[2], **OPCIONES);

for indic, ax in zip(imae, axs[0]):
    ax.set_title(indic)

for ax in axs[-1]:
    ax.set_xlabel(r'Rezago $\tau$')
    ax.set_xticks(np.arange(0,49,12));

axs[0,0].set_ylabel(r'$\log(IMAE)$')
axs[1,0].set_ylabel(r'$\Delta log(IMAE)$')
axs[2,0].set_ylabel(r'$\Delta_{12} log(IMAE)$')

fig.suptitle('Autocorrelograma parcial del IMAE (original y tendencia-ciclo) en Costa Rica', size=16);

Apuntes de Macroeconometría

Series de tiempo

Contents