3.6. Pronósticos con modelos ARMA#

Pronósticos con modelos ARMA#

Sea \(y^*_{t+j|t}\) un pronóstico de \(y_{t+j}\) pasado en datos observados hasta \(t\).

Definimos el “mejor” pronóstico de este tipo como aquel que minimiza el error cuadrático medio

\[\begin{equation*} \text{MSE}\left(y^*_{t+j|t}\right) \equiv \E\left(y_{t+j} - y^*_{t+j|t}\right)^2 \end{equation*}\]

Aunque no lo probamos aquí, resulta que el pronóstico con el menor error cuadrático medio es la esperanza de \(y_{t+j}\) condicional en los datos hasta \(t\):

\[\begin{equation*} y^*_{t+j|t} = \E\left(y_{t+j} | y_t, y_{t-1}, \dots \right) \equiv \E_t\left(y_{t+j}\right) \end{equation*}\]

Pronosticando valores puntuales de la serie#

Es muy sencillo obtener de manera recursiva estos pronósticos para los modelos ARMA, siguiendo estos 3 pasos:

Se escribe la ecuación ARMA de manera que \(y_t\) quede a la izquierda y todos los otros términos a la derecha.
Se sustituye el índice \(t\) por \(T+h\).
En el lado derecho de la ecuación, se sustituyen:

observaciones futuras con sus pronósticos,
errores futuros con cero,
errores pasados con sus respectivos residuos.

Empezando con \(h=1\), se repiten los pasos 2 y 3 para valores \(h=2,3,\dots\) hasta que todos los pronósticos hayan sido calculados.

Para ilustrar el procedimiento, consideremos este proceso ARMA(1,2)

\[\begin{equation*} (1-\phi\Lag)\tilde{y}_t = (1 + \theta_1\Lag + \theta_2\Lag^2)\epsilon_t \end{equation*}\]

Paso 1: \(\tilde{y}_t = \phi\tilde{y}_{t-1} + \epsilon_t + \theta_1\epsilon_{t-1} + \theta_2\epsilon_{t-2}\)

Para \(h=1\):

\[\begin{align*} \tilde{y}_{T+1} &= \phi\tilde{y}_{T} + \epsilon_{T+1} + \theta_1\epsilon_{T} + \theta_2\epsilon_{T-1}\\ \tilde{y}^*_{T+1|T} &= \phi\tilde{y}_{T} + \theta_1\hat{\epsilon}_{T} + \theta_2\hat{\epsilon}_{T-1} \end{align*}\]

Para \(h=2\):

\[\begin{align*} \tilde{y}_{T+2} &= \phi\tilde{y}_{T+1} + \epsilon_{T+2} + \theta_1\epsilon_{T+1} + \theta_2\epsilon_{T}\\ y^*_{T+2|T} &= \phi\tilde{y}^*_{T+1|T} + \theta_2\hat{\epsilon}_{T} \end{align*}\]

Para \(h=3\):

\[\begin{align*} \tilde{y}_{T+3} &= \phi\tilde{y}_{T+2} + \epsilon_{T+3} + \theta_1\epsilon_{T+2} + \theta_2\epsilon_{T+1}\\ y^*_{T+3|T} &= \phi\tilde{y}^*_{T+2|T} \end{align*}\]

Es fácil comprobar que, siguiendo este procedimiento, una vez que \(h>p\), \(h>q\) la ecuación de pronóstico será

\[\begin{equation*} \tilde{y}^*_{T+h} = \phi_1\tilde{y}^*_{T+h-1} + \dots + \phi_p\tilde{y}^*_{T+h-p} \end{equation*}\]

Esto es una ecuación en diferencia de orden \(p\), de la cual sabemos que sus raíces están dentro del círculo unitario. Por ello

\[\begin{align*} \lim\limits_{h\to\infty}\tilde{y}^*_{T+h} &= 0 & \text{es decir }\quad \lim\limits_{h\to\infty}y^*_{T+h} &= \mu \end{align*}\]

Esto nos dice que, para valores grandes de \(h\), el pronóstico es simplemente la media del proceso.

Cuantificando la incertidumbre de los pronósticos puntuales#

Para saber qué tan precisos esperamos que sean estos pronósticos, necesitamos cuantificar su error cuadrático medio

\[\begin{align*} \text{MSE}\left(y^*_{t+j|t}\right) &\equiv \E\left(y_{t+j} - y^*_{t+j|t}\right)^2 \\ &= \E\left(y_{t+j} - \E_t\left(y_{t+j}\right)\right)^2 \\ &= \Var_t\left(y_{t+j}\right) \end{align*}\]

Es decir, necesitamos cuantificar la varianza de \(y_{t+j}\) condicional en los datos disponibles en \(t\).

Por razones de tiempo, no vamos a desarrollar estas fórmulas durante este curso.

Ejemplo: Pronosticando la inflación

from scipy.stats import norm

plt.style.use('seaborn-dark')
horizon = 36
fcast =res.get_forecast(steps=horizon, alpha=0.05)


fig, ax =plt.subplots(figsize=[12,4])
isi.plot(ax=ax)
fcast.predicted_mean.plot(ax=ax)
ax.axhline(isi.values.mean(), color='C2')


ax.fill_between(fcast.row_labels, *fcast.conf_int().values.T,
                facecolor='C1', alpha=0.25, interpolate=True);

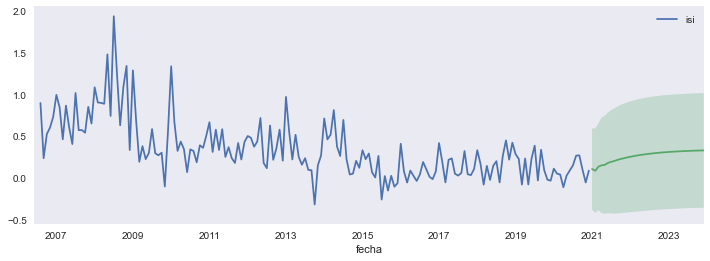
Podemos hacer intervalos de distintos niveles de significancia:

fig, ax =plt.subplots(figsize=[12,4])
isi['2018':].plot(ax=ax)
fcast.predicted_mean.plot(ax=ax)
ax.axhline(isi.values.mean(), color='C2')

for alpha in np.arange(1,6)/10:
    ax.fill_between(fcast.row_labels, *fcast.conf_int(alpha=alpha).values.T,
                facecolor='C1', alpha=0.1, interpolate=True);

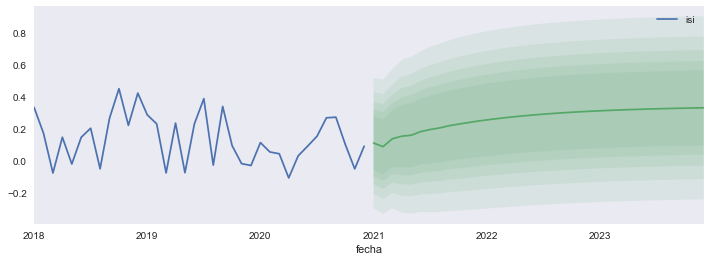
¿Qué podría salir mal?#

En todas las fórmulas que hemos elaborado para los pronósticos hasta ahora, está implícito que conocemos los verdaderos valores de los parámetros.

En la práctica, esos parámetros son estimados a partir de los datos.

Tomemos por ejemplo un proceso AR(1):

\[\begin{align*} y_{t+1} &= \phi y_t + \epsilon_{t+1} \tag{valor verdadero} \\ y^*_{t+1|t} &= \hat{\phi} y_t \tag{pronóstico} \\ &\Rightarrow \\ \notationbrace{y_{t+1} - y^*_{t+1|t}}{error de pronóstico} &= \notationbrace{\left(\phi-\hat{\phi}\right)}{“sesgo”}y_t + \notationbrace{\epsilon_{t+1}}{innovación} \end{align*}\]

Apuntes de Macroeconometría

Pronósticos con modelos ARMA

Contents

3.6. Pronósticos con modelos ARMA#

Pronósticos con modelos ARMA#

Pronosticando valores puntuales de la serie#

Cuantificando la incertidumbre de los pronósticos puntuales#

¿Qué podría salir mal?#