1.1. Descomposición del IMAE por componentes

Nota Para ejecutar este cuaderno se requiere el paquete bccr. Si no lo tiene, ejecute la siguiente celda

try:
    import bccr
except ImportError:
    print('Module bccr missing. Installing it now')
    !pip install bccr

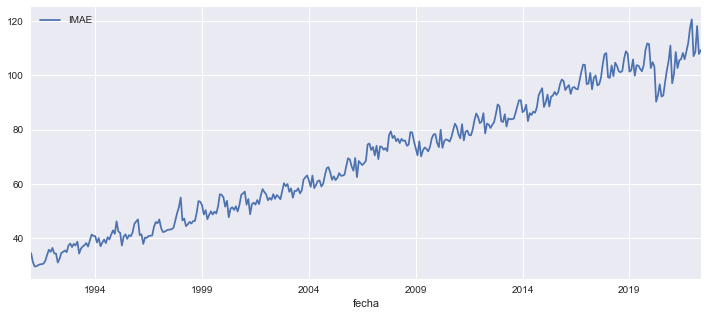
Gráfico del IMAE

from bccr import SW
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('seaborn')
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.filters.hp_filter import hpfilter

#imae = SW(IMAE=35449)  # serie anterior, no datos desde 2020-11
imae = SW(IMAE=87703)  # nueva serie
imae.plot(figsize=[12,5]);

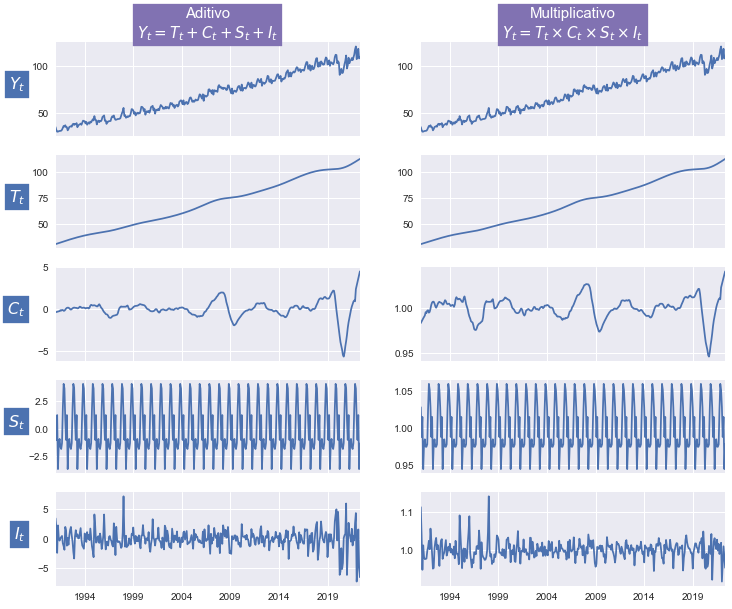
Componentes del IMAE

componentes = ['Serie\noriginal', 'Tendencia','Ciclo','Componente\nestacional','Componente\nirregular']

res = seasonal_decompose(imae, model='additive', period=12, extrapolate_trend='freq')
ciclo, tendencia = hpfilter(res.trend, lamb=14400)
additive = pd.concat([res.observed,tendencia, ciclo, res.seasonal, res.resid], axis=1)
additive.columns = componentes

res = seasonal_decompose(imae, model='multiplicative', period=12, extrapolate_trend='freq')
ciclo, tendencia = hpfilter(np.log(res.trend), lamb=14400)
multiplicative = pd.concat([res.observed, np.exp(tendencia), np.exp(ciclo), res.seasonal, res.resid], axis=1)
multiplicative.columns = componentes

descomp = pd.concat([additive, multiplicative], keys=['aditiva', 'multiplicativa'], axis=1)
descomp.index.name = ""
fig, axs = plt.subplots(5,2, figsize=[12,10], sharex=True)

for comp, ax in zip('YTCSI', axs[:,0]):
    ax.annotate(f'${comp}_t$',(-0.1,0.5), xycoords='axes fraction', ha='right', fontsize=16, color='white',backgroundcolor='C0')


for ((metodo, comp), serie), ax in zip(descomp.iteritems(), axs.T.flatten()):
    serie.plot(ax=ax)

for metodo, ax in zip(['Aditivo\n$Y_t = T_t + C_t + S_t + I_t$', 'Multiplicativo\n$Y_t = T_t \\times C_t \\times S_t \\times I_t$'], axs[0]):
    ax.annotate(metodo,(0.5,1.05), xycoords='axes fraction', ha='center', fontsize=15, color='white',backgroundcolor='C3')