\[ \begin{align}\begin{aligned}\require{color} \newcommand{\alert}[1]{{\color{RedOrange} #1}} \newcommand{\notation}[2]{\underset{\color{MidnightBlue}\text{#2}}{#1}} \newcommand{\simbolo}[2]{\underset{\color{MidnightBlue}#2}{#1}} \newcommand{\notationbrace}[2]{{\underbrace{#1}_{\color{MidnightBlue}\text{#2}}}} \DeclareMathOperator{\dd}{\,d\!} \DeclareMathOperator{\E}{\mathbb{E}{}} \DeclareMathOperator{\Var}{Var{}} \DeclareMathOperator{\Cov}{Cov{}} \DeclareMathOperator{\Lag}{L{}} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator{\Prob}{\mathbb{P}} \newcommand{\marginal}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\MAT}[1]{\begin{bmatrix} #1 \end{bmatrix}} \newcommand{\mat}[1]{\left[\begin{smallmatrix} #1 \end{smallmatrix}\right]}\\\begin{split}\DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\X}{\mathbf{x}} \DeclareMathOperator{\y}{\mathbf{y}} \DeclareMathOperator{\h}{\mathbf{h}} \newcommand{\stackEq}[1]{\MAT{#1_1 \\ #1_2 \\ \vdots \\ #1_M}} \newcommand{\e}{\mathbf{\epsilon}} \newcommand{\Y}{\mathbf{Y}} \newcommand{\estimator}[2]{{\hat{#1}^{\text{#2}}}} \newcommand{\estimate}[2]{\underset{(#2)}{#1}} \DeclareMathOperator{\plim}{plim} \newcommand{\PLIM}[2]{#1\xrightarrow{p} #2}\end{split}\end{aligned}\end{align} \]
from bccr import SW
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('seaborn')

from statsmodels.tsa.api import VAR
import statsmodels.api as sm

from itertools import permutations

8.4. Pronósticos con VAR#

Recordemos que

\[\begin{equation*} \hat{Y}_{t+s} = \xi_{t+s} + \Phi\xi_{t+s-1} +\dots+ \Phi^{s-1}\xi_{t+1} + \Phi^{s}\hat{Y}_{t} \end{equation*}\]

Suponga que \(\Phi\) ha sido estimado con datos hasta \(t=T\).

El mejor pronóstico del sistema \(s\) períodos adelante es

\[\begin{equation*} \E\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right]= \Phi^{s}\hat{Y}_{T} \end{equation*}\]

El error de pronóstico es

\[\begin{equation*} \hat{Y}_{T+s} - \E\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right]= \xi_{t+s} + \Phi\xi_{t+s-1} +\dots+ \Phi^{s-1}\xi_{t+1} \end{equation*}\]

y su varianza (MSPE) es

\[\begin{equation*} \Var\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right] = \Omega + \Phi\Omega\Phi' +\dots+ \Phi^{s-1}\Omega{\Phi'}^{s-1} \end{equation*}\]

Pronósticos de largo plazo con VAR#

Partiendo de

\[\begin{equation*} \E\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right]= \Phi^{s}\hat{Y}_{T} \end{equation*}\]

recordamos que:

  • \(\hat{y}_t\equiv y_t-\mu\)

  • si el VAR es estacionario, \(\lim\limits_{s\to\infty}\Phi^s = 0\).

Entonces el pronóstico de largo plazo

\[\begin{equation*} \lim\limits_{s\to\infty}\E\left[Y_{T+s} - \mathbf{\mu} \;|\; \hat{Y}_{T}\right]= \lim\limits_{s\to\infty}\Phi^{s}\hat{Y}_{T} = 0 \end{equation*}\]

es decir

\[\begin{equation*} \lim\limits_{s\to\infty}\E\left[y_{T+s} \;|\; \hat{Y}_{T}\right]= \mu \end{equation*}\]

en el largo plazo el VAR volverá a su equilibrio estacionario.

Descomposición de la varianza del shock reducido#

Recuerde que los errores reducidos están relacionados con los estructurales por \(\epsilon_t = \Gamma_0^{-1}\varepsilon_t\).

Sea \(\Gamma_0^{-1} \equiv A =\MAT{a_1&\dots&a_n}\), con \(a_i\) la \(i\)-ésima columna de \(i\).

Entonces

\[\begin{align*} \epsilon_t &= a_1\varepsilon_{1t} + a_2\varepsilon_{2t} + \dots + a_n\varepsilon_{nt} \\ \Omega = \E[\epsilon_t\epsilon'_t] &= \sigma_1^2 a_1a'_1 + \sigma_2^2 a_2a'_2 +\dots +\sigma_n^2 a_na'_n \\ &= \sum_{j=1}^{n} \sigma_j^2 a_ja'_j \end{align*}\]

Ejemplo:   {Descomposición de \(\Omega\)}

Tomando \(\Omega\) del ejemplo al inicio de este capítulo

\[\begin{equation*} \begin{aligned} \Omega = \MAT{1 & 0.5 & -1 \\ 0.5 & 4.25 & 2.5\\ -1 & 2.5 & 12.25} &=\simbolo{\MAT{1 & 0 & 0\\ 0.5 & 1 & 0\\-1 & 0.75 & 1}}{\Gamma_0^{-1}} \simbolo{\MAT{1 & 0 & 0\\ 0 & 4 & 0 \\0 & 0 & 9}}{\Sigma} \simbolo{\MAT{1 & 0.5 & -1\\ 0 & 1 & 0.75 \\0 & 0 & 1}}{{\Gamma'}_0^{-1}} \end{aligned} \end{equation*}\]

Entonces \(a'_1 = \MAT{1 & 0.5 & -1}\), \(a'_2 = \MAT{0 & 1 & 0.75}\), \(a'_3 = \MAT{0 & 0 & 1}\) y

\[\begin{align*} \Omega &= 1 \MAT{1 \\ 0.5 \\ -1}\MAT{1 & 0.5 & -1} + 4\MAT{0 \\ 1 \\ 0.75}\MAT{0 & 1 & 0.75} + 9\MAT{0 \\ 0 \\ 1}\MAT{0 & 0 & 1} \\ &= \simbolo{1}{\sigma_1^2}\simbolo{\MAT{1 &0.5 & -1\\ 0.5&0.25& -0.5\\-1&-0.5&1}}{a_1a'_1} + \simbolo{4}{\sigma_2^2}\simbolo{\MAT{0&0&0\\ 0&1&0.75\\ 0&0.75& 0.5625}}{a_2a'_2} + \simbolo{9}{\sigma_3^2}\simbolo{\MAT{0&0&0\\0&0&0\\0&0&1}}{a_3a'_3} \end{align*}\]

Observe que esta descomposición depende del ordenamiento de las variables.

Descomposición de la varianza del pronóstico#

Sustituyendo \(\Omega = \sum_{j=1}^{n} \sigma_j^2 a_ja'_j\) en \(\Var\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right] \) tenemos

\[\begin{multline*} \Var\left[\hat{Y}_{T+s}\;|\; \hat{Y}_{T}\right] = \\ \sum_{j=1}^{n} \sigma_j^2 \left\{a_ja'_j + \Phi a_ja'_j\Phi' + \dots + \Phi^{s-1}a_ja'_j{\Phi'}^{s-1} \right\} \end{multline*}\]

Con esta expresión, podemos cuantificar la contribución del \(j\)-ésimo shock estructural al error cuadrático medio del pronóstico \(s\)-períodos adelante.

Warning

Observe que esto asume que conocemos los parámetros del modelo: ¡No toma en cuenta los errores de estimación!}

Ejemplo:   Un modelo VAR para la política monetaria de Costa Rica
Supongamos que queremos ver el papel que juega la tasa de política monetaria \(R\) del BCCR sobre el desempleo \(u\) y la inflación \(\pi\) en nuestro país.

Para ello estimaremos un VAR:

\[\begin{equation*} \MAT{u_{t} \\ \pi_{t} \\ R_{t}} = \MAT{c_1 \\ c_2 \\ c_3} + \sum_{i=1}^{p} \notation{\Phi_i}{$3\times 3$}\MAT{u_{t-i} \\ \pi_{t-i} \\ R_{t-i}} + \MAT{\epsilon^u_t \\ \epsilon^\pi_t \\ \epsilon^R_t} \end{equation*}\]

Contamos con una muestra de 39 observaciones trimestrales, de 2010-III a 2020-I.

datos = SW(Desempleo=22796, Inflación=25485, TPM=3541, freq='Q', func=np.mean, fillna='ffill')['2010Q3':'2020Q1']
nombres = datos.columns

fig, ax = plt.subplots(figsize=[12, 6])
datos.plot(ax=ax)
ax.set(title='Desempleo, inflación y tasa de política monetaria',
       ylabel='puntos porcentuales');
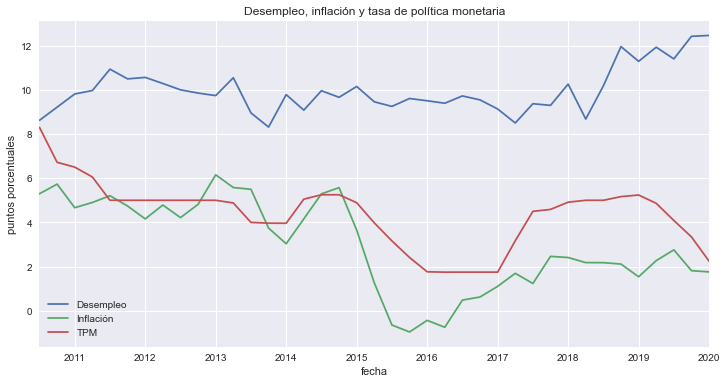
../../_images/04-pronostico_3_1.png

Escogiendo número de rezagos

El primer paso es escoger el número de rezagos \(p\) del VAR:

model = VAR(datos)
model.select_order(4).summary()
VAR Order Selection (* highlights the minimums)
AIC BIC FPE HQIC
0 1.227 1.360 3.411 1.273
1 -1.779 -1.246* 0.1693 -1.595
2 -2.121* -1.188 0.1219* -1.799*
3 -2.007 -0.6741 0.1411 -1.547
4 -2.002 -0.2689 0.1511 -1.404

En este ejemplo escogeremos un solo rezago, en parte porque tenemos una muestra muy pequeña.

Estimando el VAR

res = model.fit(maxlags=1)
res.summary()

  Summary of Regression Results   
==================================
Model:                         VAR
Method:                        OLS
Date:           Thu, 21, Jul, 2022
Time:                     00:36:36
--------------------------------------------------------------------
No. of Equations:         3.00000    BIC:                   -1.30856
Nobs:                     38.0000    HQIC:                  -1.64170
Log likelihood:          -115.071    FPE:                   0.161485
AIC:                     -1.82569    Det(Omega_mle):        0.119601
--------------------------------------------------------------------
Results for equation Desempleo
===============================================================================
                  coefficient       std. error           t-stat            prob
-------------------------------------------------------------------------------
const                2.305139         1.265376            1.822           0.069
L1.Desempleo         0.708084         0.125437            5.645           0.000
L1.Inflación        -0.127880         0.087455           -1.462           0.144
L1.TPM               0.243191         0.124252            1.957           0.050
===============================================================================

Results for equation Inflación
===============================================================================
                  coefficient       std. error           t-stat            prob
-------------------------------------------------------------------------------
const               -0.062525         1.588872           -0.039           0.969
L1.Desempleo        -0.003928         0.157505           -0.025           0.980
L1.Inflación         0.827925         0.109813            7.539           0.000
L1.TPM               0.119255         0.156017            0.764           0.445
===============================================================================

Results for equation TPM
===============================================================================
                  coefficient       std. error           t-stat            prob
-------------------------------------------------------------------------------
const                2.282890         0.964744            2.366           0.018
L1.Desempleo        -0.164187         0.095635           -1.717           0.086
L1.Inflación         0.091391         0.066677            1.371           0.170
L1.TPM               0.753419         0.094732            7.953           0.000
===============================================================================

Correlation matrix of residuals
             Desempleo  Inflación       TPM
Desempleo     1.000000  -0.031396 -0.003364
Inflación    -0.031396   1.000000  0.307269
TPM          -0.003364   0.307269  1.000000

Causalidad de Granger

Al parecer, ninguna variable del sistema causa a otra en el sentido de Granger.

Valores p de hipótesis de causalidad:

granger = pd.DataFrame(
  [[res.test_causality(i, j).pvalue for i in nombres] for j in nombres],
  index = nombres,
  columns=nombres)
granger.index.name = 'Explicativa'
granger.columns.name = 'Dependiente'

granger.round(3)
Dependiente Desempleo Inflación TPM
Dependiente
Desempleo 0.000 0.980 0.089
Inflación 0.147 0.000 0.173
TPM 0.053 0.446 0.000

Esto no necesariamente implica que no haya relación de causalidad entre las variables: podría haber causalidad contemporánea.

Funciones de impulso-respuesta con impulsos unitarios

Funciones de impulso respuesta, con impulsos unitarios.

res.irf(10).plot(subplot_params={'figsize':[12,4]});
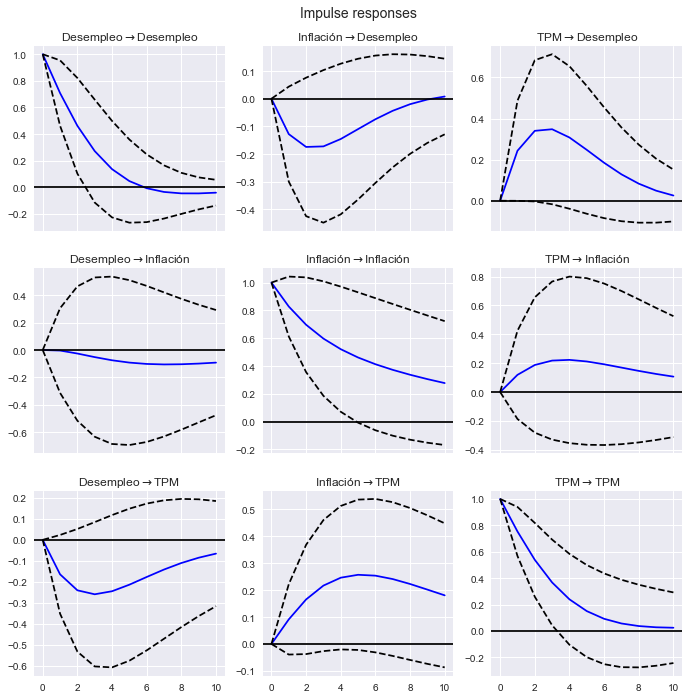
../../_images/04-pronostico_11_0.png

Funciones de impulso-respuesta con impulsos ortogonales

El resultado depende del ordenamiento de las variables en el sistema (Choleski).

def respuesta_politica(orden, h=20):
    res = VAR(datos[[*orden]]).fit(1)
    irfs = pd.DataFrame(res.irf(h).orth_irfs.reshape(h+1,-1),
                        columns = pd.MultiIndex.from_product(
                            [orden, orden],
                            names=['Respuesta', 'Impulso']
                        )
                       )

    series = ['Desempleo', 'Inflación']                   
    efectos = irfs.xs('TPM', level='Impulso', axis=1)[series]
    reacciones = irfs.xs('TPM', level='Respuesta', axis=1)[series]
    return efectos, reacciones

fig1, axs1 = plt.subplots(2,1, figsize=[12,8], sharex=True)
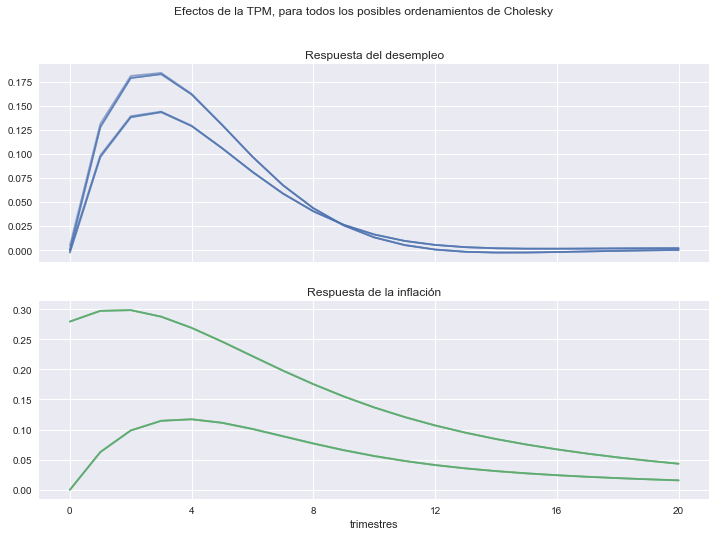
fig1.suptitle('Efectos de la TPM, para todos los posibles ordenamientos de Cholesky')   

fig2, axs2 = plt.subplots(2,1, figsize=[12,8], sharex=True)
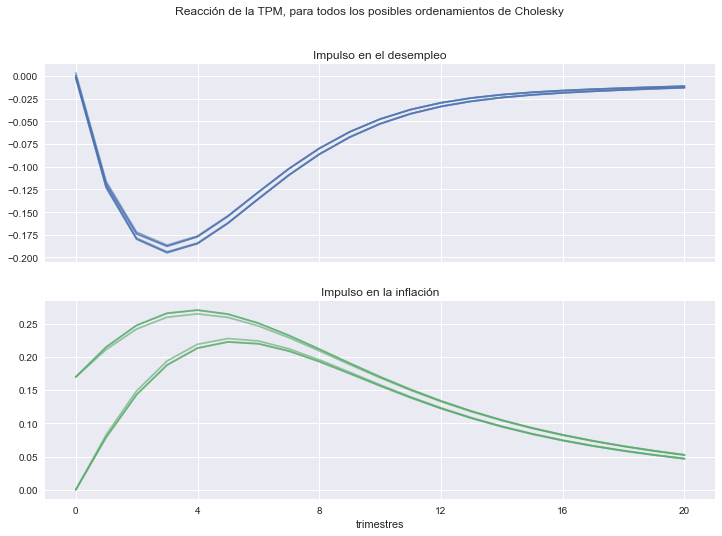
fig2.suptitle('Reacción de la TPM, para todos los posibles ordenamientos de Cholesky')   


for orden in permutations(nombres):
    efectos, reacciones = respuesta_politica(orden)
    efectos.plot(subplots=True, ax=axs1, legend=False, alpha=0.6)
    reacciones.plot(subplots=True, ax=axs2, legend=False, alpha=0.6)

axs1[0].set(title='Respuesta del desempleo')
axs1[1].set(title='Respuesta de la inflación',
           xlabel='trimestres',
           xticks=np.arange(0,21,4));

axs2[0].set(title='Impulso en el desempleo')
axs2[1].set(title='Impulso en la inflación',
          xlabel='trimestres',
          xticks=np.arange(0,21,4));
../../_images/04-pronostico_13_0.png ../../_images/04-pronostico_13_1.png

Pronosticando con el VAR

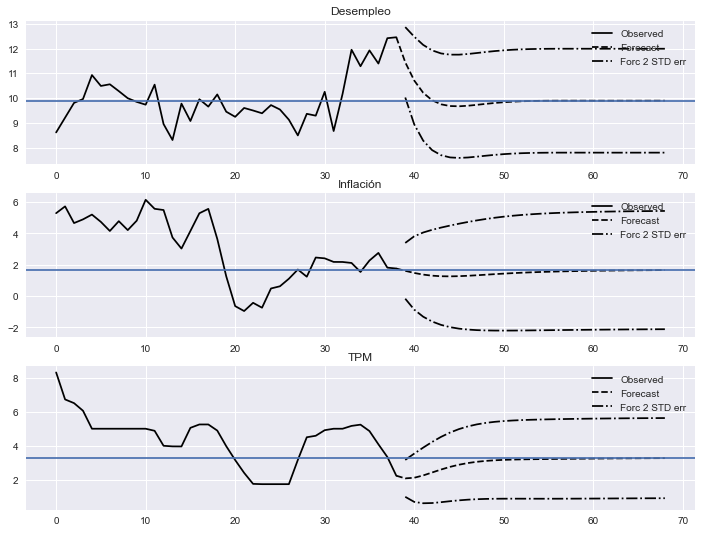
En un VAR estacionario, los pronósticos siempre convergen a la media de largo plazo de cada variable:

\[\begin{equation*} \mu = \left(I - \Phi_1 - \Phi_2 \dots - \Phi_p\right)^{-1}c \end{equation*}\]
fig = res.plot_forecast(30);
fig.set_size_inches([12,9])

𝜇 = np.linalg.solve(np.eye(3) - res.coefs.sum(axis=0), res.intercept)
for ax, v in zip(fig.get_axes(), 𝜇):
    ax.axhline(v)
../../_images/04-pronostico_15_0.png

Warning

El valor de \(\mu\) no coincide necesariamente con el promedio simple de los datos.

pd.DataFrame({'𝜇':𝜇, 'Promedio datos': datos.mean()})
𝜇 Promedio datos
Dependiente
Desempleo 9.899185 9.978157
Inflación 1.693923 2.983095
TPM 3.294578 4.365460

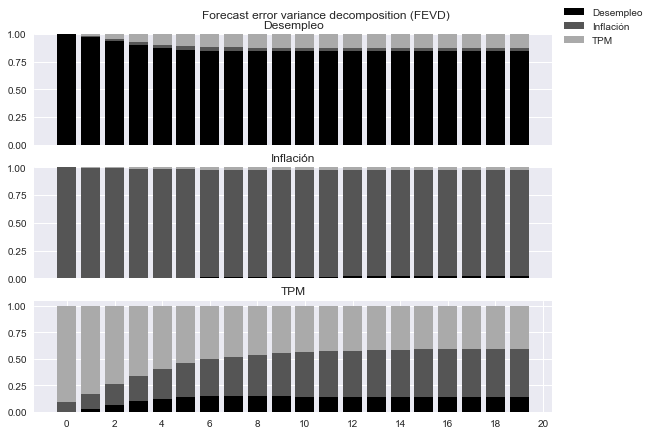
Descomposición de la varianza de pronóstico

fig=res.fevd(20).plot(figsize=[9,6]);
fig.axes[0].set(xticks=[])
fig.axes[1].set(xticks=[])
fig.axes[2].set(xticks=np.arange(0,21,2))
for ax in fig.axes:
    ax.set(yticks=[0,0.25,0.5,0.75,1.0])
../../_images/04-pronostico_19_0.png