Estimación de un modelo ARMA de inflación para Costa Rica
Contents
3.1. Estimación de un modelo ARMA de inflación para Costa Rica#
Nota Para ejecutar este cuaderno se requiere el paquete bccr. Si no lo tiene, ejecute la siguiente celda
try:
import bccr
except ImportError:
print('Module bccr missing. Installing it now')
!pip install bccr
Descarga de datos#
from bccr import SW
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import numpy as np
import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
SW.buscar(todos='inflación subyacente')
| DESCRIPCION | Unidad | Medida | periodo | |
|---|---|---|---|---|
| codigo | ||||
| 1264 | Índices de Precios/Indice Subyacente de inflación (ISI), (Julio 2006 = 100) [1264]' | Nivel | NO DEFINIDO | Mensual |
| 1267 | Índices de Precios/Indice Subyacente de inflación (ISI), (Julio 2006 = 100) [1267]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 24167 | Índices de Precios/Inflación subyacente por exclusión [24167]' | Nivel | NaN | Mensual |
| 24170 | Índices de Precios/Inflación subyacente reponderada por persistencia [24170]' | Nivel | NaN | Mensual |
| 24172 | Índices de Precios/Inflación subyacente reponderada por persistencia [24172]' | Porcentaje Variación Interanual | Unidades | Mensual |
| 24173 | Índices de Precios/Inflación subyacente reponderada por volatilidad [24173]' | Nivel | NaN | Mensual |
| 24175 | Índices de Precios/Inflación subyacente reponderada por volatilidad [24175]' | Porcentaje Variación Interanual | Unidades | Mensual |
| 25721 | Índices de Precios/Indicadores de Inflación Subyacente, (Junio 2015 = 100) [25721]' | Nivel | NaN | Mensual |
| 25725 | Índices de Precios/IEV [25725]' | Porcentaje Variación Mensual | NO DEFINIDO | Mensual |
| 25726 | Índices de Precios/IEV [25726]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 25728 | Índices de Precios/IMT [25728]' | Porcentaje Variación Mensual | NO DEFINIDO | Mensual |
| 25729 | Índices de Precios/IMT [25729]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 25731 | Índices de Precios/IRV [25731]' | Porcentaje Variación Mensual | NO DEFINIDO | Mensual |
| 25732 | Índices de Precios/IRV [25732]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 25734 | Índices de Precios/IRP [25734]' | Porcentaje Variación Mensual | NO DEFINIDO | Mensual |
| 25735 | Índices de Precios/IRP [25735]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 25737 | Índices de Precios/IEF [25737]' | Porcentaje Variación Mensual | NO DEFINIDO | Mensual |
| 25738 | Índices de Precios/IEF [25738]' | Porcentaje Variación Interanual | NO DEFINIDO | Mensual |
| 90267 | Índices de Precios/Inflación subyacente, promedio dic 2020=100 [90267]' | Nivel | NaN | Mensual |
| 90268 | Índices de Precios/Inflación subyacente, promedio dic 2020=101 [90268]' | Porcentaje Variación Mensual | NaN | Mensual |
| 90269 | Índices de Precios/Inflación subyacente, promedio dic 2020=102 [90269]' | Porcentaje Variación Interanual | NaN | Mensual |
isi = SW(isi=25725).dropna()
isi
| isi | |
|---|---|
| fecha | |
| 2006-08 | 0.895052 |
| 2006-09 | 0.236138 |
| 2006-10 | 0.524076 |
| 2006-11 | 0.601677 |
| 2006-12 | 0.730769 |
| ... | ... |
| 2020-08 | 0.266575 |
| 2020-09 | 0.270565 |
| 2020-10 | 0.099647 |
| 2020-11 | -0.053413 |
| 2020-12 | 0.088659 |
173 rows × 1 columns
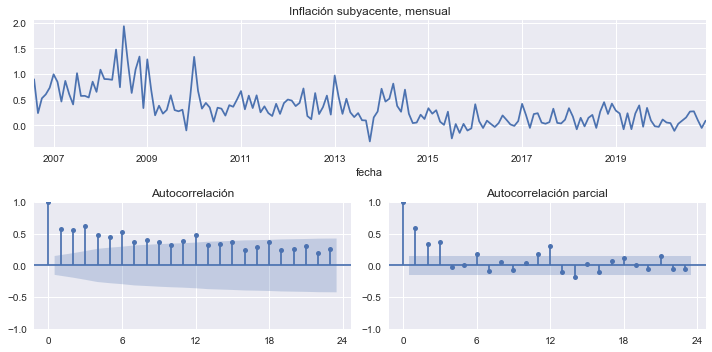
Graficar la serie original y estudiar su autocorrelograma#
fig, axs = plt.subplot_mosaic(
"""
AA
BC
""", figsize=[10,5], tight_layout=True)#, sharey='row')
isi.plot(ax=axs['A'], title='Inflación subyacente, mensual', legend=None)
plot_acf(isi, ax=axs['B'], title='Autocorrelación')
plot_pacf(isi, ax=axs['C'], title='Autocorrelación parcial');
axs['B'].set_xticks(range(0,30,6))
axs['C'].set_xticks(range(0,30,6))
axs['C'].sharey(axs['B'])
fig.savefig('ISI-AR3.pdf', bbox_inches='tight')
Estimar un modelo AR(3)#
res = ARIMA(isi, order=[3,0,0]).fit()
res.summary()
| Dep. Variable: | isi | No. Observations: | 173 |
|---|---|---|---|
| Model: | ARIMA(3, 0, 0) | Log Likelihood | -4.734 |
| Date: | Thu, 21 Jul 2022 | AIC | 19.468 |
| Time: | 00:14:26 | BIC | 35.234 |
| Sample: | 08-31-2006 | HQIC | 25.864 |
| - 12-31-2020 | |||
| Covariance Type: | opg |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.3406 | 0.116 | 2.939 | 0.003 | 0.113 | 0.568 |
| ar.L1 | 0.2630 | 0.069 | 3.787 | 0.000 | 0.127 | 0.399 |
| ar.L2 | 0.1983 | 0.050 | 3.998 | 0.000 | 0.101 | 0.296 |
| ar.L3 | 0.3646 | 0.069 | 5.270 | 0.000 | 0.229 | 0.500 |
| sigma2 | 0.0615 | 0.005 | 12.753 | 0.000 | 0.052 | 0.071 |
| Ljung-Box (L1) (Q): | 0.01 | Jarque-Bera (JB): | 96.24 |
|---|---|---|---|
| Prob(Q): | 0.94 | Prob(JB): | 0.00 |
| Heteroskedasticity (H): | 0.23 | Skew: | 1.11 |
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 5.90 |
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Exportar la tabla de coeficientes a LaTeX#
sss = res.summary()
with open('AR3-ISI.tex','w') as file:
file.write(sss.tables[1].as_latex_tabular())
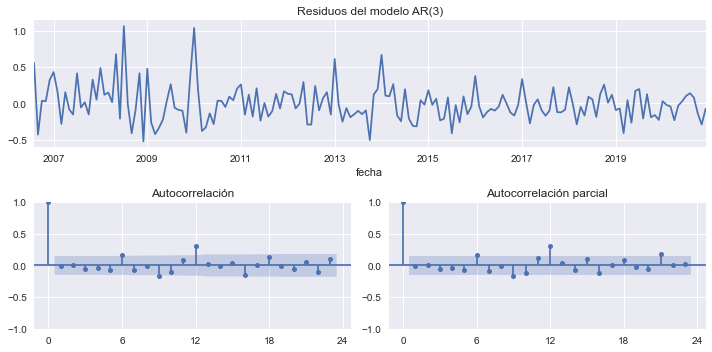
Analizar los residuos#
fig, axs = plt.subplot_mosaic(
"""
AA
BC
""", figsize=[10,5], tight_layout=True)#, sharey='row')
res.resid.plot(ax=axs['A'], title='Residuos del modelo AR(3)', legend=None)
plot_acf(res.resid, ax=axs['B'], title='Autocorrelación')
plot_pacf(res.resid, ax=axs['C'], title='Autocorrelación parcial')
axs['B'].set_xticks(range(0,30,6))
axs['C'].set_xticks(range(0,30,6))
axs['C'].sharey(axs['B'])
fig.savefig('ISI-AR3resid.pdf', bbox_inches='tight')
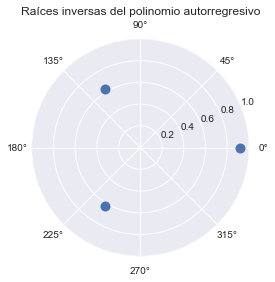
Raíces del polinomio característico (recíprocos de las raíces del polinomio de rezagos)#
1 / res.arroots
array([ 0.91510159+0.j , -0.32602757+0.5404744j,
-0.32602757-0.5404744j])
arroots = 1/res.arroots
plt.polar(np.angle(arroots), np.abs(arroots), '.', ms=20)
fig = plt.gcf()
ax = fig.gca()
ax.set_rlim([0,1])
ax.set_title('Raíces inversas del polinomio autorregresivo')
fig.savefig('ISI-AR3roots.pdf', bbox_inches='tight')
Usar criterios de selección para determinar el grado p, q del modelo ARMA#
pmax = 4
qmax = 2
P = np.arange(pmax+1)
Q = np.arange(qmax+1)
Akaike#
aic = [[ARIMA(isi, order=[p,0,q]).fit().aic for q in Q ] for p in P ]
AIC = pd.DataFrame(aic, index=[f'p={p}' for p in P], columns=[f'q={q}' for q in Q])
AIC.style.highlight_min()
| q=0 | q=1 | q=2 | |
|---|---|---|---|
| p=0 | 131.620888 | 89.023411 | 82.401382 |
| p=1 | 60.759065 | 25.081481 | 26.533141 |
| p=2 | 41.690410 | 26.708214 | 28.697323 |
| p=3 | 19.467588 | 21.346944 | 23.220068 |
| p=4 | 21.338571 | 23.338547 | 19.543282 |
Exportar a LATEX
AIC.round(2).to_latex('ISI-AR3aic.tex')
Bayesiano#
bic = [[ARIMA(isi, order=[p,0,q]).fit().bic for q in Q ] for p in P ]
BIC = pd.DataFrame(bic, index=[f'p={p}' for p in P], columns=[f'q={q}' for q in Q])
BIC.style.highlight_min()
| q=0 | q=1 | q=2 | |
|---|---|---|---|
| p=0 | 137.927471 | 98.483286 | 95.014549 |
| p=1 | 70.218940 | 37.694647 | 42.299599 |
| p=2 | 54.303577 | 42.474672 | 47.617073 |
| p=3 | 35.234046 | 40.266694 | 45.293109 |
| p=4 | 40.258321 | 45.411589 | 44.769614 |
Exportar a LATEX
BIC.round(2).to_latex('ISI-AR3bic.tex')
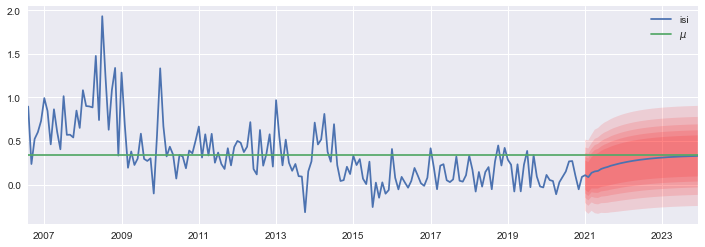
Pronóstico#
horizon = 36
temp = res.get_prediction(start=isi.index[-1] + pd.offsets.MonthEnd(), end='2023-12', dynamic=False, index=None, exog=None, extend_model=None, extend_kwargs=None)
ff, std, conf = temp.predicted_mean, temp.se_mean, temp.conf_int(0.05)
#ff, std, conf = res.forecast(steps=horizon, alpha=0.05) # version anterior, no funciona con el nuevo módulo de ARIMA
Valores críticos de la distribución normal#
from scipy.stats import norm
alpha = np.arange(1,6)/10
zvalues = norm(0, 1).isf(np.array(alpha)/2)
Graficar el pronóstico#
# Datos pronosticados
fcast = pd.DataFrame({'isi':ff,'std':std}, index=pd.period_range(isi.index[-1]+1, periods=horizon, freq='M'))
# Concatenar los datos observados con los pronosticados
fcast2 = pd.concat([isi,fcast], sort=False)
fcast2['$\mu$'] = isi.values.mean()
# Graficar la serie y el pronóstico
fig, ax =plt.subplots(figsize=[12,4])
fcast2[['isi','$\mu$']].plot(ax=ax)
def intervalo(z):
"""
Para calcular los límites superior e inferior del intervalo de confianza,
dado el valor crítico de la distribución normal
"""
return fcast2['isi']+z*fcast2['std'], fcast2['isi']-z*fcast2['std']
# fechas para graficar los intervalos
d = fcast2.index.values
# Graficar los intervalos de confianza
for z in zvalues:
ax.fill_between(d, *intervalo(z), facecolor='red', alpha=0.12, interpolate=True)
fig.savefig('ISI-AR3forecast.pdf', bbox_inches='tight')
Exportar datos a STATA#
isi.index = isi.index.to_series().astype(str)
isi.to_stata('isi.dta')


