Raíces unitarias estacionales
Contents
6.4. Raíces unitarias estacionales#
Diferenciación estacional y raíces unitarias#
Si para modelar una serie estacional es necesario aplicar el operador \(\Delta_s=(1-\Lag^s)\), entonces la serie original tiene una raíz unitaria estacional: \(1-1^s = 0\).
Pero 1 no es la única raíz de \(1-\Lag^s\): al ser este un polinomio de grado \(s\), tiene exactamente \(s\) raíces (no necesariamente todas reales):
o bien, usando la fórmula de Euler
Todas estas raíces están equidistanciadas en la circunferencia unitaria.
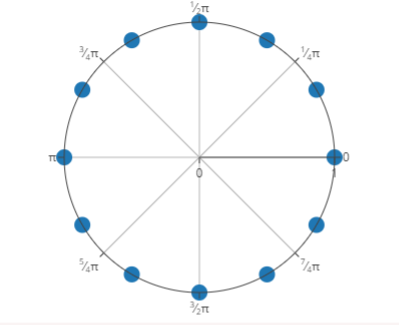
\(\cos\left(\frac{k\pi}{6}\right) + i\sin\left(\frac{k\pi}{6}\right)\)
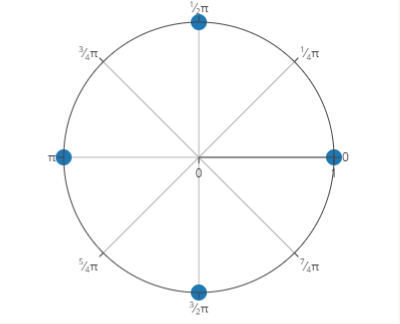
\(\cos\left(\frac{k\pi}{2}\right) + i\sin\left(\frac{k\pi}{2}\right)\)
Pruebas de raíz unitaria estacional#
La literatura provee varias pruebas para detectar raíces unitarias. Una de ellas es la prueba de Dickey, Hasza y Fuller (DHF, 1984), la cual es una extensión de la prueba Dickey Fuller:
Al igual que en la prueba DF, la hipótesis nula es \(\gamma=0\) contra la alternativa \(\gamma <0\), aunque los valores críticos son distintos.
Una limitación de esta prueba es que no es apropiada para diagnosticar la presencia de las otras raíces unitarias estacionales.
Existen otras pruebas de raíces unitarias estacionales
La prueba HEGY de Hylleberg, Engle, Granger, y Yoo (1990)
La prueba de Kunst (1997)
La prueba OCSB, de Osborn, Chui, Smith y Birchenhall (1988)
La prueba CH, de Canova y Hansen (1995)
Sin embargo, no estudiaremos estas pruebas en este curso.
