4.3. Series con raíz unitaria y procesos ARIMA#

Series con raíz unitaria#

La caminata aleatoria (con o sin deriva) puede verse como un modelo AR(1) en el cual la raíz del polinomio de rezagos es uno:

\[\begin{align*} y_t &= c + y_{t-1} + \epsilon_t \\ (1-\Lag)y_t &= c + \epsilon_{t} \end{align*}\]

Por ello, en general decimos que un proceso con tendencia estocástica tiene raíz unitaria.

Consideremos el siguiente proceso AR(2)

\[\begin{equation*} y_t = 0.6y_{t-1} + 0.4y_{t-2} + \epsilon_{t} \end{equation*}\]

Su polinomio de rezagos es \(1-0.6\Lag - 0.4\Lag^2 = (1-0.4\Lag)(1-1\Lag)\), cuyas raíces son 1 y 2.5. Es decir, este proceso también tiene una raíz unitaria, y por tanto no es estacionario.

La factorización del polinomio de rezagos nos sugiere escribir

\[\begin{align*} (1-0.4\Lag)(1-1\Lag)y_t & =\epsilon_{t} \\ (1-0.4\Lag)\Delta y_t & =\epsilon_{t} \\ \Delta y_t & = 0.4\Delta y_{t-1} + \epsilon_{t} \end{align*}\]

Visto como un proceso para \(y^*\equiv\Delta y_t\), este es un proceso AR(1) estacionario.

Procesos ARIMA(p,d,q)#

En el ejemplo anterior, como la primera diferencia de \(y_t\) es un proceso AR(1) estacionario, decimos que \(y_t\) es un proceso ARIMA(1,1,0).

En general, si un proceso integrado de orden \(d\), \(y_t\), es diferenciado \(d\) veces y su resultado \(\Delta^d y_t\) es un proceso ARMA(p,q), entonces decimos que \(y_t\) tiene un proceso ARIMA(p,d,q):

{admonition} Autorregresivo integrado de media móvil: ARIMA Sea \(\left\{\epsilon_t\right\}\) ruido blanco; el proceso estocástico \vspace{-0.5em}

\[\begin{equation*} \Phi(\Lag)(1-\Lag)^d y_t = \Theta(\Lag)\epsilon_t \end{equation*}\]

\vspace{-0.5em} es llamado proceso ARIMA(p,d,q), donde \(\Phi(\Lag)\) es un polinomio de grado \(p\) cuyas raíces están fuera del círculo unitario, y \(\Theta(\Lag)\) es un polinomio de grado \(q\).

Repaso del modelo clásico de regresión lineal#

En el modelo clásico de regresión lineal se tiene

\[\begin{equation*} y_i = \beta_1x_{1,i} + \beta_2x_{2,i} + \dots + \beta_kx_{k,i} + \epsilon_i \end{equation*}\]

donde \(\epsilon_i\sim N(0,\sigma^2)\) es un error homoscedástico y no-autocorrelacionado.

Si se cumplen los supuestos del MCRL, este modelo se puede estimar de manera insesgada y eficiente por medio del estimador mínimos cuadrados ordinarios.

Para hacer un test sobre un parámetro

\[\begin{align*} H_0:\quad \beta_j &= q & H_1:\quad \beta_j &\neq q \end{align*}\]

utilizamos el valor estimado por mínimos cuadrados ordinarios \(\hat{\beta}_j\) y su error estándar \(s.e.(\beta_j)\), y decimos que si la hipótesis nula es cierta entonces el estadístico

\[\begin{equation*} \frac{\hat{\beta}_j - q}{s.e.(\beta_j)} \sim t_{n-k} \end{equation*}\]

(tiene una distribución \(t\)-Student con \(n-k\) grados de libertad, donde \(n\) es el número de observaciones y \(k\) el número de parámetros estimados).

Es decir, con un nivel de significancia \(\alpha\), el intervalo

\[\begin{equation*} \left[q + t_{\alpha/2}s.e.(\beta_j),\; q + t_{1-\alpha/2}s.e.(\beta_j)\right] \end{equation*}\]

contendrá al valor estimado \(\hat{\beta}_j\) en \(100(1-\alpha)\%\) de las muestras siempre y cuando sea cierto que \(\beta_j=q\).

Por ello, cuando encontramos un valor \(\hat{\beta}_j\) que no está contenido en ese intervalo, rechazamos la hipótesis nula, y decimos que \(\beta_j\) es significativamente distinto de \(q\), a sabiendas de que nuestro procedimiento incurrirá en el error tipo-1 (rechazar una hipotésis verdadera) en \(100\alpha\%\) de las muestras.

Para que este procedimiento tenga validez, es necesario que el estadístico efectivamente tenga la distribución \(t\)-Student, lo cual es cierto siempre que se cumplan los supuestos del modelo clásico de regresión lineal.

Regresión espuria#

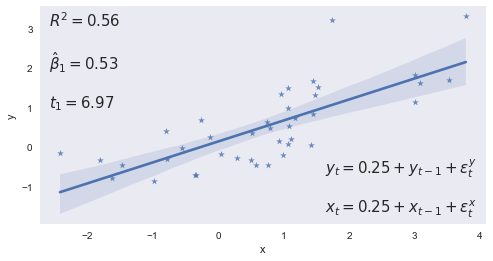
En 1974, Granger y Newbold demostraron, via simulaciones, que si una serie I(1) se estima en función de otra serie I(1) completamente independiente de ella, los estadísticos usuales tenderán a mostar que las dos series están relacionadas.

Es decir, si \(y_t, x_t\) son dos series I(1) independientes, al correr la regresión

\[\begin{equation*} y_t = \beta_0 + \beta_1 x_t + \epsilon_{t} \end{equation*}\]

fallaríamos en rechazar la hipótesis nula \(\beta_1 = 0\) (la cual es cierta porque \(y_t\) no depende de \(x_t\)) con una frecuencia mayor a la que sugiere la distribución \(t\)-student correspondiente:

\[\begin{equation*} \frac{\hat{\beta}_{1}}{\hat{s.e}(\beta_1)} \sim t_{T-2} \quad\Leftarrow\text{¡ya no es cierto!} \end{equation*}\]

Este fenómeno de encontrar relaciones inexistentes entre variables integradas se conoce como regresión espuria.

Ejemplo: Replicando Granger y Newbold 1974

\[\begin{align*} y_t &= 0.25 + y_{t-1} + \epsilon^y_t \\ x_t &= 0.25 + x_{t-1} + \epsilon^x_t \end{align*}\]

np.random.seed(240)
e = np.random.randn(40,2)

df = pd.DataFrame(
    (0.25+e).cumsum(axis=1),
    columns=['y', 'x']
    )

res = smf.ols("y ~ x" , df).fit()

fig, ax = plt.subplots(figsize=[8,4])
sns.regplot(x='x',y='y',data=df, marker='*',ax=ax)
ax.set(xlabel='x', ylabel='y')

statslabel = f'$R^2={res.rsquared:.2f}$'
statslabel += f'\n\n$\\hat\\beta_1={res.params[1]:.2f}$'
statslabel += f'\n\n$t_1={res.tvalues[1]:.2f}$'
ax.annotate(statslabel, (0.02,0.98), xycoords='axes fraction', size=15, va='top')

modellabel = r'$y_t = 0.25 + y_{t-1} + \epsilon^y_t$'
modellabel += '\n\n$x_t = 0.25 + x_{t-1} + \\epsilon^x_t$'
ax.annotate(modellabel, (0.98,0.02), xycoords='axes fraction', size=15, va='bottom',ha='right')
ax.grid(False);

../../_images/03-raices-unitarias_3_0.png

res.summary()

OLS Regression Results
Dep. Variable:	y	R-squared:	0.561
Model:	OLS	Adj. R-squared:	0.550
Method:	Least Squares	F-statistic:	48.60
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	2.69e-08
Time:	00:15:57	Log-Likelihood:	-40.091
No. Observations:	40	AIC:	84.18
Df Residuals:	38	BIC:	87.56
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	0.1400	0.119	1.174	0.248	-0.101	0.381
x	0.5325	0.076	6.972	0.000	0.378	0.687

Omnibus:	7.474	Durbin-Watson:	2.329
Prob(Omnibus):	0.024	Jarque-Bera (JB):	6.173
Skew:	0.843	Prob(JB):	0.0457
Kurtosis:	3.929	Cond. No.	1.94

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

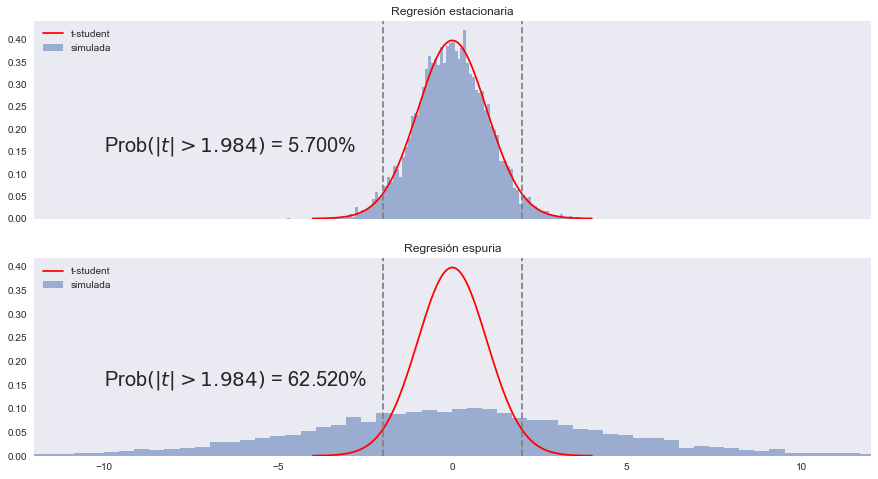
Experimento de Monte Carlo para determinar la distribución del estadítico t

%%time
def regresion(T=40):
    e = np.random.randn(2, T)

    df = pd.DataFrame(dict(
        x = e[0].cumsum(),
        y = e[1].cumsum(),
        u = e[0],
        v = e[1]
        ),
        columns=['x', 'y', 'u', 'v']
        )

    t_estacionario = smf.ols("v~u", data=df).fit().tvalues[1]
    t_espurio = smf.ols("y~x", data=df).fit().tvalues[1]
    return t_estacionario, t_espurio

def Monte_Carlo(funcion, repeticiones, columns, *args, **kwargs):
    datos = Parallel(n_jobs=-1)(delayed(funcion)(*args, **kwargs) for _ in range(repeticiones))
    return pd.DataFrame(datos, columns=columns)


N = 10_000
np.random.seed(12345)
tvalues = Monte_Carlo(regresion, N, ['estacionaria', 'espuria'])


maxtval = 12
t5crit = t_Student.isf(0.05/2, 98)


fig, (ax0,ax1) = plt.subplots(2,1,figsize=[15, 8], sharex=True)


def plot_simulated(caso, ax):
    ff, edges = np.histogram(tvalues[caso], bins=100, density=True)
    center = (edges[1:] + edges[:-1])/2
    w = center[1] - center[0]

    ax.bar(center, ff, width=w, alpha=0.5)
    xvals = np.linspace(-4,4, 200)
    ax.plot(xvals, t_Student.pdf(xvals, df=98), '-r')
    ax.set(xlim=[-maxtval, maxtval], title=f'Regresión {caso}')
    ax.legend(['t-student', 'simulada'], loc='upper left')

    # valores críticos
    opciones = dict(ls="--", color='gray')
    ax.axvline(t5crit, **opciones)
    ax.axvline(-t5crit, **opciones)

    # error tipo I
    err1 = (tvalues[caso].abs() > t5crit).mean()*100
    ax.annotate(f'Prob$\\left(|t| > 1.984\\right)$ = {err1:.3f}%', (-10,0.15), size=20)

    ax.grid(False)

    
plot_simulated('estacionaria', ax0)
plot_simulated('espuria', ax1)

CPU times: total: 51.7 s
Wall time: 2min 7s

../../_images/03-raices-unitarias_6_1.png

Regresión lineal con series integradas#

¿Cómo estudiar la relación entre series integradas sin incurrir en regresiones espurias?

Supongamos que tanto \(y_t\) como \(x_t\) son series I(1).

Entonces, por definición, \(\Delta y_t\) y \(\Delta x_t\) son series estacionarias.

En tal caso, el modelo

\[\begin{equation*} \Delta y_t = \beta_0 + \beta_1\Delta x_t + \epsilon_t \end{equation*}\]

puede estimarse por mínimos cuadrados, y la prueba \(\beta_1=0\) se realiza usando el procedimiento usual.

Una alternativa mejor, que estudiaremos con detalladamente más tarde en el curso, es estimar la regresión en niveles

\[\begin{equation*} y_t = \beta_0 + \beta_1 x_t + \epsilon_t \end{equation*}\]

y determinar si los residuos de esta regresión son estacionarios. Si lo son, diremos que \(y_t\) está cointegrada con \(x_t\).

Procesos AR(p) con raíz unitaria#

Recordemos que el proceso AR(p) puede escribirse

\[\begin{align*} y_t & = c + \phi_1 y_{t-1} +\dots + \phi_p y_{t-p} + \epsilon_t \\ \left(1 - \phi_1\Lag^1 -\dots - \phi_p\Lag^p\right)y_{t} & = c + \epsilon_t \\ \Phi(\Lag)y_{t} & = c + \epsilon_t \end{align*}\]

Supongamos que los coeficientes autorregresivos suman uno. Entonces

\[\begin{align*} \Phi(1) &= 1 - \phi_1 1^1 -\dots - \phi_p 1^p\\ &= 1 - (\phi_1 + \phi_2 + \dots + \phi_p) = 1 - 1 = 0 \end{align*}\]

Es decir, si \(\phi_1 + \phi_2 + \dots + \phi_p=1\), entonces el proceso tiene raíz unitaria.

Apuntes de Macroeconometría

Series con raíz unitaria y procesos ARIMA

Contents