Regresión espuria
Contents
9.1. Regresión espuria#
Estos apuntes tienen por objetivo ilustrar el problema que surge de estimar modelos de regresión lineal con series de tiempo no estacionarias (regresión espuria).
En primer lugar, se estima una regresión en la que el PIB per capita de Costa Rica depende del de Malta (a priori, no esperaríamos que el PIB per capita de Malta tenga impacto en el de Costa Rica). Más adelante, realizamos experimentos de Monte Carlo para analizar las consecuencias de estimar regresiones con datos no estacionarios.
Preparación#
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from statsmodels.api import OLS
from statsmodels.formula.api import ols
pd.set_option('display.float_format',lambda x: '%.2f' % x)
plt.style.use('seaborn')
GITHUB_REPO = "https://raw.githubusercontent.com/randall-romero/econometria/master/data/"
DATAPATH = GITHUB_REPO if 'google.colab' in str(get_ipython()) else '../data/'
Necesitamos importar una clase de un módulo local. Para ello, usualmente es suficiente con tener el módulo (archivo py) en la misma carpeta que este cuaderno, pero eso no funcionaría cuando se corre en Colab. Por ello, añadimos explícitamente la carpeta que contiene ese módulo en el path de Python.
import sys
sys.path.insert(1, DATAPATH)
from mackinnon import MacKinnon # este módulo contiene herramientas para calcular valores críticos de MacKinnon
La función AEG acá definida realizará la prueba (aún no Aumentada) de Engle y Granger a partir de los residuos de una regresión
mk = MacKinnon()
def AEG(residuals, N, summary=True):
'''Prueba de cointegración de Engle y Granger'''
aux = OLS(residuals.diff(), residuals.shift(1), missing='drop').fit()
t = aux.tvalues[0]
nobs = aux.nobs
crit = mk('c', N, T=nobs)
if summary:
print('Prueba de cointegración de Engle y Granger')
print('ADF stat = %.3f\nCritical values:' % t)
for k, v in crit.items():
print('\t%5s: %.3f' % (k,v))
if t < crit['1%']:
print('Series están cointegradas (al 1% significancia)')
elif t < crit['5%']:
print('Series están cointegradas (al 5% significancia)')
elif t < crit['10%']:
print('Series están cointegradas (al 10% significancia)')
else:
print('Series no están cointegradas')
return t
Regresión con datos de Costa Rica y de Malta#
Los datos fueron obtenidos directamente del Banco Mundial, usando el paquete wbdata.
data = pd.read_pickle("https://github.com/randall-romero/econometria/raw/master/data/datos-CRI-MLT.pickle")
Reading data from datos-CRI-MLT.pickle.
Cargados los datos, los graficamos y mostramos las últimas 8 observaciones en una tabla.
data.plot()
data.tail(8)
| country | CRI | MLT |
|---|---|---|
| date | ||
| 2012 | 8689.97 | 21691.26 |
| 2013 | 8785.74 | 22375.04 |
| 2014 | 8993.53 | 23842.23 |
| 2015 | 9219.39 | 25798.47 |
| 2016 | 9509.74 | 26645.86 |
| 2017 | 9732.27 | 27669.37 |
| 2018 | 9889.74 | 28594.30 |
| 2019 | NaN | NaN |
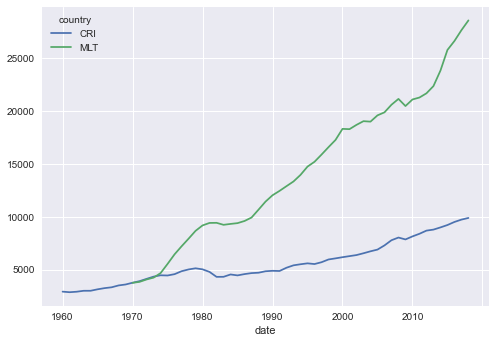
Los datos originales están en niveles. Para la regresión $\( \log(CRI) = c + \log(MLT) + \epsilon \)$
se necesita calcular el logaritmo de cada serie. Acá simplemente hacemos una base nueva ldata a partir de la original.
ldata = np.log(data)
Ahora sí, estimamos la regresión con el función ols. Nótese que según los resultados, un aumento de un punto porcentual en el PIB de Malta está asociado con una disminución de 0.4494 pp en Costa Rica; el resultado es estadísticamente significativo.
model = ols('CRI ~ MLT',ldata)
resultados = model.fit()
resultados.summary()
| Dep. Variable: | CRI | R-squared: | 0.806 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.802 |
| Method: | Least Squares | F-statistic: | 195.0 |
| Date: | Sun, 24 Apr 2022 | Prob (F-statistic): | 2.40e-18 |
| Time: | 11:58:04 | Log-Likelihood: | 34.197 |
| No. Observations: | 49 | AIC: | -64.39 |
| Df Residuals: | 47 | BIC: | -60.61 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 4.4814 | 0.300 | 14.916 | 0.000 | 3.877 | 5.086 |
| MLT | 0.4432 | 0.032 | 13.966 | 0.000 | 0.379 | 0.507 |
| Omnibus: | 57.494 | Durbin-Watson: | 0.064 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 5.218 |
| Skew: | 0.156 | Prob(JB): | 0.0736 |
| Kurtosis: | 1.432 | Cond. No. | 164. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(resultados.summary())
OLS Regression Results
==============================================================================
Dep. Variable: CRI R-squared: 0.806
Model: OLS Adj. R-squared: 0.802
Method: Least Squares F-statistic: 195.0
Date: Sun, 24 Apr 2022 Prob (F-statistic): 2.40e-18
Time: 11:58:04 Log-Likelihood: 34.197
No. Observations: 49 AIC: -64.39
Df Residuals: 47 BIC: -60.61
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 4.4814 0.300 14.916 0.000 3.877 5.086
MLT 0.4432 0.032 13.966 0.000 0.379 0.507
==============================================================================
Omnibus: 57.494 Durbin-Watson: 0.064
Prob(Omnibus): 0.000 Jarque-Bera (JB): 5.218
Skew: 0.156 Prob(JB): 0.0736
Kurtosis: 1.432 Cond. No. 164.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Ahora bien, observe que los residuos no parecen ser ruido blanco.
resultados.resid.plot()
<AxesSubplot:xlabel='date'>
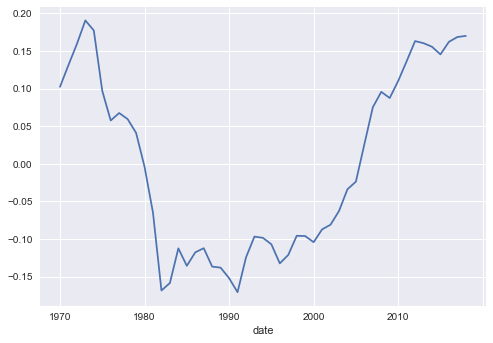
Esto lo podemos confirmar con la prueba de Dickey y Fuller. Dado que al parecer los residuos tienen raíz unitaria, podemos inferir que el PIB de Costa Rica no está cointegrado con el de Malta.
t=AEG(resultados.resid, 2)
Prueba de cointegración de Engle y Granger
ADF stat = -0.532
Critical values:
1%: -4.138
5%: -3.470
10%: -3.130
Series no están cointegradas
Ahora bien, nótese que el problema de regresión espuria (casi) desaparece una vez corremos la regresión con series estacionarias (en este caso, el crecimiento en cada país).
modeldiff = ols('CRI ~ MLT',ldata.diff())
modeldiff.fit().summary()
| Dep. Variable: | CRI | R-squared: | 0.032 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.011 |
| Method: | Least Squares | F-statistic: | 1.537 |
| Date: | Sun, 24 Apr 2022 | Prob (F-statistic): | 0.221 |
| Time: | 11:58:04 | Log-Likelihood: | 102.51 |
| No. Observations: | 48 | AIC: | -201.0 |
| Df Residuals: | 46 | BIC: | -197.3 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.0143 | 0.006 | 2.269 | 0.028 | 0.002 | 0.027 |
| MLT | 0.1378 | 0.111 | 1.240 | 0.221 | -0.086 | 0.362 |
| Omnibus: | 27.205 | Durbin-Watson: | 1.244 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 58.241 |
| Skew: | -1.586 | Prob(JB): | 2.26e-13 |
| Kurtosis: | 7.365 | Cond. No. | 26.4 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
print(modeldiff.fit().summary())
OLS Regression Results
==============================================================================
Dep. Variable: CRI R-squared: 0.032
Model: OLS Adj. R-squared: 0.011
Method: Least Squares F-statistic: 1.537
Date: Sun, 24 Apr 2022 Prob (F-statistic): 0.221
Time: 11:58:04 Log-Likelihood: 102.51
No. Observations: 48 AIC: -201.0
Df Residuals: 46 BIC: -197.3
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0143 0.006 2.269 0.028 0.002 0.027
MLT 0.1378 0.111 1.240 0.221 -0.086 0.362
==============================================================================
Omnibus: 27.205 Durbin-Watson: 1.244
Prob(Omnibus): 0.000 Jarque-Bera (JB): 58.241
Skew: -1.586 Prob(JB): 2.26e-13
Kurtosis: 7.365 Cond. No. 26.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Simulación de datos#
Ahora, vamos a definir una función para simular dos caminatas aleatorias con intercepto, calibradas con la media y la desviación estándar del crecimiento en ambos países.
growth = ldata.diff().mean()
print('El crecimiento medio es:')
print(growth)
sigma = ldata.diff().std()
print('\ny las respectivas volatilidades son:')
print(sigma)
El crecimiento medio es:
country
CRI 0.02
MLT 0.04
dtype: float64
y las respectivas volatilidades son:
country
CRI 0.03
MLT 0.04
dtype: float64
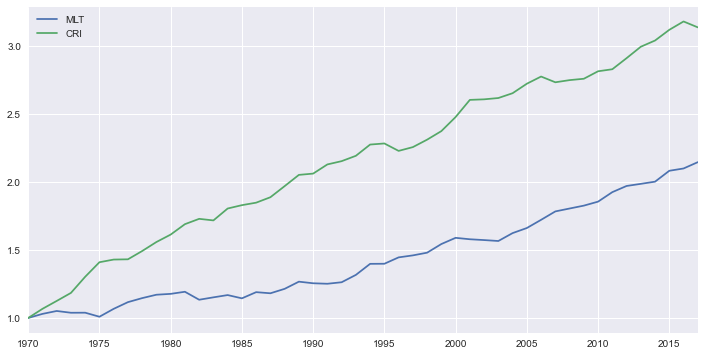
Para las simulaciones, fijamos el tamaño de muestra en T=48. Observe que las dos series que se crean son independientes.
T = 48
calendario = pd.date_range(start='1970',freq='A',periods=T)
def generate_series():
X = np.ones((T,2))
for t in range(1, T):
X[t] = X[t-1] + growth + sigma * np.random.randn(2)
return pd.DataFrame(X,index=calendario, columns=['MLT','CRI'])
Aquí simulamos el proceso una vez para ver que parezca razonable.
datos_simulados = generate_series()
datos_simulados.plot(figsize=[12,6])
<AxesSubplot:>
resultados_simulados = ols('CRI ~ MLT',datos_simulados).fit().summary()
resultados_simulados
| Dep. Variable: | CRI | R-squared: | 0.910 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.908 |
| Method: | Least Squares | F-statistic: | 464.6 |
| Date: | Sun, 24 Apr 2022 | Prob (F-statistic): | 1.11e-25 |
| Time: | 11:58:06 | Log-Likelihood: | 13.619 |
| No. Observations: | 48 | AIC: | -23.24 |
| Df Residuals: | 46 | BIC: | -19.50 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -0.2903 | 0.117 | -2.477 | 0.017 | -0.526 | -0.054 |
| MLT | 1.7084 | 0.079 | 21.555 | 0.000 | 1.549 | 1.868 |
| Omnibus: | 2.562 | Durbin-Watson: | 0.137 |
|---|---|---|---|
| Prob(Omnibus): | 0.278 | Jarque-Bera (JB): | 2.329 |
| Skew: | -0.452 | Prob(JB): | 0.312 |
| Kurtosis: | 2.410 | Cond. No. | 9.29 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Monte Carlo#
from joblib import Parallel, delayed
def Monte_Carlo(funcion, repeticiones, columnas, *args, **kwargs):
"""
Ejecuta simulaciones de Montecarlo en paralelo, aprovechando todos los núcleos del procesador
Argumentos:
funcion: una función que dé por resultado una única realización de las cantidades que se desean simular
repeticiones: un entero que indica cuántas muestras se desean simular
columnas: una lista (o tupla) de strings, que identifiquen a las cantidades individuales retornadas por funcion
*args, **kwargs: otros parámetros requeridos por funcion
Retorna:
Un data frame de pandas, con tantas filas como `repeticiones` y columnas como textos en `columnas`.
"""
datos = Parallel(n_jobs=-1)(delayed(funcion)(*args, **kwargs) for _ in range(repeticiones))
return pd.DataFrame(datos, columns=columnas)
Para la simulación de Monte Carlo, veremos el parámetro asociado con MLT, así como su estadístico t y el valor p. Para facilitar la labor, definimos una función que extrae estos tres estadísticos de los resultados de una regresión y los retorna como una lista. Añadimos ademas el p-value de la prueba aumentada de Dickey-Fuller respecto a si los residuos de la regresión presentan raices unitarias.
def give_me_the_summary(res):
statistics = ['params', 'tvalues', 'pvalues']
tval = AEG(res.resid, 2,False)
return [getattr(res, k)['MLT'] for k in statistics] + [tval]
Para cada iteración del experimento de Monte Carlo, generamos una nueva muestra con generate_series(), luego estimamos el modelo con los datos en niveles (resultados en rl) y en primeras diferencias (rd). Retornamos los seis estadísticos correspondientes.
Recuerde que, por construcción, las series en primera diferencia sí son estacionarias.
def simulate_regression():
data = generate_series()
rl = ols('CRI ~ MLT', data).fit()
rd = ols('CRI ~ MLT', data.diff()).fit()
return give_me_the_summary(rl) + give_me_the_summary(rd)
Fijamos el número de repeticiones en nrep=1000 y creamos una tabla (pd.DataFrame) con los resultados de todas las simulaciones.
%%time
nrep = 10000 # number of repetitions
montecarlo = Monte_Carlo(simulate_regression, nrep, columnas=pd.MultiIndex.from_product([['LEVEL','DIFF'], ['coeff','t-stat', 'p-value', 'tvalue-res']]))
Wall time: 2min 23s
Finalmente, analizamos la distribución de cada uno de los estadísticos bajo consideración.
ax = montecarlo.swaplevel(axis=1).hist(layout=(4,2), figsize=[12,12],bins=20)
mk('c', 2, T)
Level
1% -4.14
5% -3.47
10% -3.13
dtype: float64
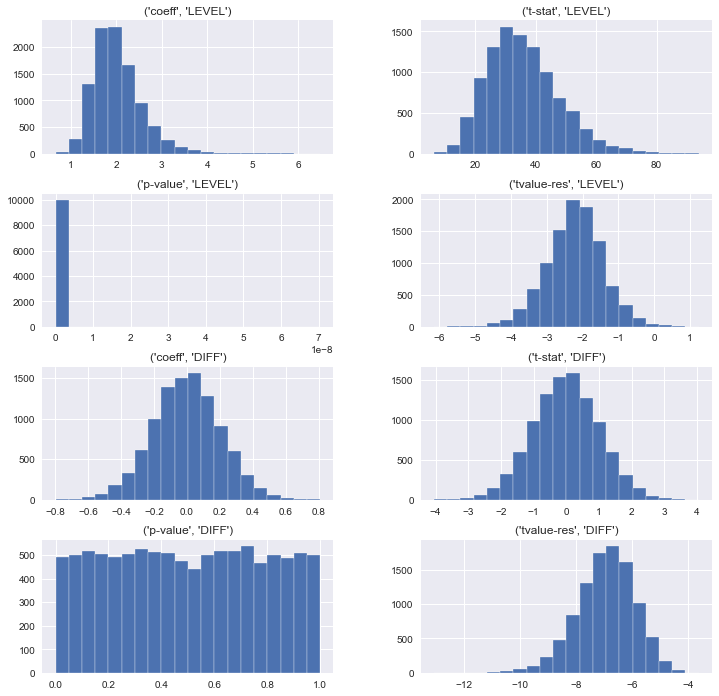
Puede verse para las regresiones en niveles, siempre encontramos una asociación positiva y estadísticamente significativa entre las dos series, a pesar de que son independientes! En contraste, cuando las regresiones se realizan con datos estacionarios (primeras diferencias), rutinariamente rechazaríamos la hipótesis de que el PIB de Malta está correlacionado con el de Costa Rica.


