3.2. Estimación de la demanda de dinero#

Nota Para ejecutar este cuaderno se requiere el paquete bccr. Si no lo tiene, ejecute la siguiente celda

try:
    import bccr
except ImportError:
    print('Module bccr missing. Installing it now')
    !pip install bccr

from bccr import SW
import numpy as np
from matplotlib import rcParams
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import matplotlib.gridspec as gridspec

import statsmodels.api as sm
from statsmodels.formula.api import ols

plt.style.use('seaborn')

# Cambiar tamaño de las fuentes
rcParams['axes.titlesize'] = 20
rcParams['axes.labelsize'] = 16
rcParams['xtick.labelsize'] = 14
rcParams['ytick.labelsize'] = 14

SW.buscar('medio circulante')

	DESCRIPCION	Unidad	Medida	periodo
codigo
608	Sector Monetario y Financiero/Medio circulante [608]'	Colón Costarricense	NaN	Mensual

SW.buscar('tasa básica pasiva', frecuencia='D')

	DESCRIPCION	Unidad	Medida	periodo
codigo
3748	Tasas de interés/Tasa básica pasiva [3748]'	Porcentaje	NaN	Diaria

variables = dict(IMAE=35449,IPC=25482,M1=1445,Tbasica=423)
datos = SW(**variables, func='mean', FechaInicio='1991m01', FechaFinal='2020m11').dropna()
datos

	IMAE	IPC	M1	Tbasica
fecha
1991-01	51.108817	8.064069	6.158123e+04	34.000000
1991-02	42.665858	8.301969	6.024168e+04	35.000000
1991-03	40.391637	8.407419	5.942290e+04	33.193548
1991-04	40.185649	8.644489	6.078601e+04	33.000000
1991-05	40.276545	8.794029	6.185368e+04	32.500000
...	...	...	...	...
2020-07	110.987099	106.127077	5.166828e+06	3.708065
2020-08	110.584336	106.122788	5.206881e+06	3.635484
2020-09	113.705524	106.411930	5.206211e+06	3.498333
2020-10	118.613059	106.496597	5.061595e+06	3.293548
2020-11	120.969090	106.498184	4.913216e+06	3.346667

359 rows × 4 columns

res = ols('M1 ~ IMAE + IPC + Tbasica', data=np.log(datos)).fit()

fig = plt.figure(figsize=[10,5], tight_layout=True)
gs = gridspec.GridSpec(2, 2)
ax = fig.add_subplot(gs[0, :])
axs0 = fig.add_subplot(gs[1,0])
axs1 = fig.add_subplot(gs[1,1], sharey=axs0)

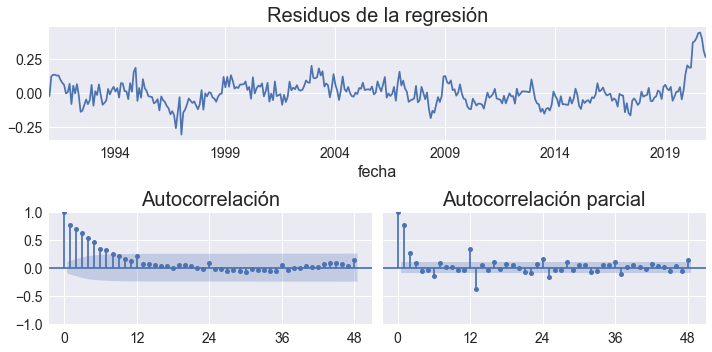
res.resid.plot(title='Residuos de la regresión', ax=ax)

OPCIONES = dict(lags=48, alpha=0.05, )
sm.graphics.tsa.plot_acf(res.resid, ax=axs0, title='Autocorrelación',**OPCIONES);
sm.graphics.tsa.plot_pacf(res.resid, ax=axs1, title='Autocorrelación parcial', **OPCIONES);
axs0.set_xticks([0,12,24,36,48])
axs1.set_xticks([0,12,24,36,48])

fig.savefig('residuos-demanda-dinero.pdf', bbox_inches='tight')

sss = res.summary()
sss

OLS Regression Results
Dep. Variable:	M1	R-squared:	0.994
Model:	OLS	Adj. R-squared:	0.994
Method:	Least Squares	F-statistic:	1.944e+04
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	0.00
Time:	00:15:30	Log-Likelihood:	335.36
No. Observations:	359	AIC:	-662.7
Df Residuals:	355	BIC:	-647.2
Df Model:	3
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	6.3294	0.298	21.263	0.000	5.744	6.915
IMAE	1.0242	0.079	13.044	0.000	0.870	1.179
IPC	0.9268	0.028	33.508	0.000	0.872	0.981
Tbasica	-0.3519	0.022	-15.919	0.000	-0.395	-0.308

Omnibus:	115.244	Durbin-Watson:	0.450
Prob(Omnibus):	0.000	Jarque-Bera (JB):	463.868
Skew:	1.349	Prob(JB):	1.87e-101
Kurtosis:	7.872	Cond. No.	390.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

sss.tables[2]

Omnibus:	115.244	Durbin-Watson:	0.450
Prob(Omnibus):	0.000	Jarque-Bera (JB):	463.868
Skew:	1.349	Prob(JB):	1.87e-101
Kurtosis:	7.872	Cond. No.	390.

sss = res.summary()

with open('regresion-M1.tex','w') as file:
    file.write(sss.tables[1].as_latex_tabular())
    file.write(sss.tables[2].as_latex_tabular())

Apuntes de Macroeconometría

Estimación de la demanda de dinero

3.2. Estimación de la demanda de dinero#