Estimación del modelo I de Klein por Mínimos Cuadrados en 2 etapas (2SLS)
Contents
7.1. Estimación del modelo I de Klein por Mínimos Cuadrados en 2 etapas (2SLS)#
import pandas as pd, numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
%matplotlib inline
Descripción del modelo y preparación de los datos#
En este laboratorio presentamos el Modelo I de Klein (1950), el cual es un ejemplo ampliamente utilizado de un modelo de ecuaciones simultáneas.
El modelo es:
Consumo:
\[\begin{equation*}
C_t = a_0 + a_1 P_t + a_2 P_{t-1} + a_3(Wp_t + Wg_t) + e_{1t}
\end{equation*}\]
Inversión:
\[\begin{equation*}
I_t = b_0 + b_1 P_t + b_2 P_{t-1} + b_3 K_{t-1} + e_{2t}
\end{equation*}\]
Salarios privados:
\[\begin{equation*}
Wp_t = g_0 + g_1 X_t + g_2 X_{t-1} + g_3 A_t + e_{3t}
\end{equation*}\]
Equilibrio demanda:
\[\begin{equation*}
X_t = C_t + I_t + G_t
\end{equation*}\]
Utilidades privadas:
\[\begin{equation*}
P_t = X_t - T_t - Wp_t
\end{equation*}\]
Stock de capital:
\[\begin{equation*}
K_t = K_{t-1} + I_{t-1}
\end{equation*}\]
Las variables endógenas son las que aparecen del lado izquierdo. Las exógenas son:
\(G_t\) = gasto (no salarial) del gobierno
\(T_t\) = impuestos indirectos a las empresas + exportaciones netas
\(Wg_t\) = gastos salarial del gobierno
\(A_t\) = tendecia, años desde 1931
Hay tres variables predeterminadas: los rezagos del stock de capital, utilidades privadas, y demanda total.
El modelo contiene 3 ecuaciones de comportamiento, una condición de equilibrio, y dos identidades contables.
En este laboratorio replicaremos el trabajo de Klein, quien estimó este modelo con datos de 1921 a 1941.
Referencia: Greene 2012 Econometric Analysis. Prentice Hall, 7th edition. Pages 332-333
Leyendo los datos#
klein = pd.read_fwf("https://github.com/randall-romero/econometria/raw/master/data/TableF10-3.txt")
klein.dropna(inplace=True)
klein['Year'] = klein['Year'].astype(int)
klein.index = pd.period_range(start=klein['Year'].iloc[0], periods=klein.shape[0], freq="A")
del klein['Year']
datanames = dict(C="consumo",
P="utilidades corporativas",
Wp="salarios sector privado",
I="inversión",
K1="stock de capital del año anterior",
X="producto nacional bruto",
Wg="salarios sector público",
G="gasto del gobierno",
T="impuestos")
klein.rename(columns=datanames).plot(subplots=True, figsize=[12,9], layout=[-1,3]);
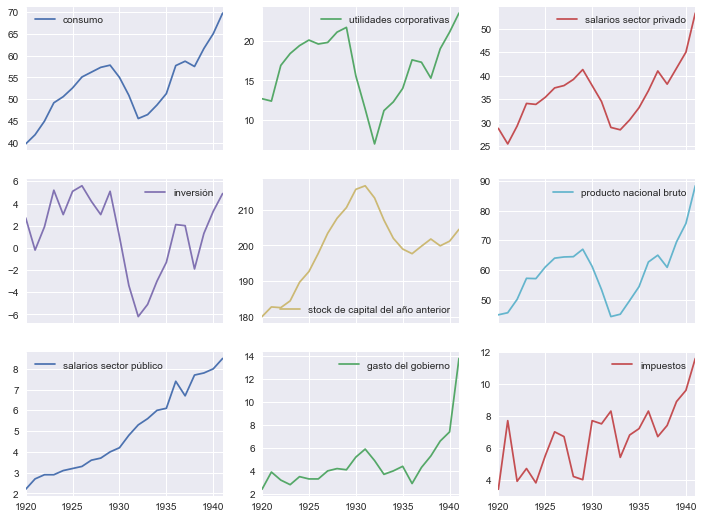
Series adicionales#
La variable K1 en la base de datos corresponde al rezago del capital, por lo que generamos K. Además, generamos la tendencia y el intercepto.
#klein['K'] = klein['K1'].shift(-1)
klein['A'] = np.arange(klein.shape[0]) - 11
klein['interc'] = 1
Generamos las variables predeterminadas y la suma de salarios
klein['P1'] = klein['P'].shift(1)
klein['X1'] = klein['X'].shift(1)
klein['W'] = klein['Wp'] + klein['Wg']
klein.dropna(inplace=True)
Preparando las regresiones#
Luego clasificamos las variables en tres grupos: endógenas, exogenas, y predeterminadas
endogenas = ['C', 'I', 'Wp', 'X', 'P']
exogenas = ['interc', 'G', 'T', 'Wg', 'A']
predeterminadas = ['K1', 'P1', 'X1']
regresores_eqs = [['interc', 'P', 'P1', 'W'], ['interc', 'P', 'P1', 'K1'], ['interc', 'X', 'X1', 'A']]
Etapa 1: regresión de las endógenas contra todas las exógenas del sistema#
Y = klein[endogenas]
X = klein[exogenas+predeterminadas]
beta = np.linalg.solve(X.T@X, X.T@Y)
beta = pd.DataFrame(beta, columns=endogenas, index=exogenas+predeterminadas)
yhat = X@beta
Etapa 2#
Definir lista de instrumentos para cada ecuación:
Esta lista es igual a la lista de regresores original, pero sustituyendo las endógenas por su valor ajustado de la etapa 1
klein_ols = pd.concat([yhat, klein[exogenas+predeterminadas]], axis=1)
klein_ols['W'] = klein_ols['Wp'] + klein_ols['Wg']
coef2sls = []
for xx, yy in zip(regresores_eqs, endogenas[:3]):
X1, y1 = klein_ols[xx], klein_ols[yy]
beta1 = np.linalg.solve(X1.T@X1, X1.T@y1)
coef2sls.append(pd.Series(beta1.ravel(), index=xx, name=yy))
pd.concat(coef2sls, axis=1, sort=False).round(3)
| C | I | Wp | |
|---|---|---|---|
| interc | 16.555 | 20.278 | 1.500 |
| P | 0.017 | 0.150 | NaN |
| P1 | 0.216 | 0.616 | NaN |
| W | 0.810 | NaN | NaN |
| K1 | NaN | -0.158 | NaN |
| X | NaN | NaN | 0.439 |
| X1 | NaN | NaN | 0.147 |
| A | NaN | NaN | 0.130 |
Mismo modelo, pero usando statsmodels#
from statsmodels.sandbox.regression.gmm import IV2SLS
for xx, yy in zip(regresores_eqs, endogenas[:3]):
fit = IV2SLS(klein[yy], klein[xx], instrument=X).fit()
print(fit.summary())
IV2SLS Regression Results
==============================================================================
Dep. Variable: C R-squared: 0.977
Model: IV2SLS Adj. R-squared: 0.973
Method: Two Stage F-statistic: 225.9
Least Squares Prob (F-statistic): 6.82e-14
Date: Thu, 21 Jul 2022
Time: 00:33:21
No. Observations: 21
Df Residuals: 17
Df Model: 3
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
interc 16.5548 1.468 11.277 0.000 13.458 19.652
P 0.0173 0.131 0.132 0.897 -0.260 0.294
P1 0.2162 0.119 1.814 0.087 -0.035 0.468
W 0.8102 0.045 18.111 0.000 0.716 0.905
==============================================================================
Omnibus: 0.768 Durbin-Watson: 1.485
Prob(Omnibus): 0.681 Jarque-Bera (JB): 0.741
Skew: 0.209 Prob(JB): 0.691
Kurtosis: 2.180 Cond. No. 282.
==============================================================================
IV2SLS Regression Results
==============================================================================
Dep. Variable: I R-squared: 0.885
Model: IV2SLS Adj. R-squared: 0.865
Method: Two Stage F-statistic: 41.20
Least Squares Prob (F-statistic): 5.15e-08
Date: Thu, 21 Jul 2022
Time: 00:33:21
No. Observations: 21
Df Residuals: 17
Df Model: 3
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
interc 20.2782 8.383 2.419 0.027 2.591 37.965
P 0.1502 0.193 0.780 0.446 -0.256 0.556
P1 0.6159 0.181 3.404 0.003 0.234 0.998
K1 -0.1578 0.040 -3.930 0.001 -0.243 -0.073
==============================================================================
Omnibus: 5.033 Durbin-Watson: 2.085
Prob(Omnibus): 0.081 Jarque-Bera (JB): 2.880
Skew: -0.800 Prob(JB): 0.237
Kurtosis: 3.856 Cond. No. 5.01e+03
==============================================================================
IV2SLS Regression Results
==============================================================================
Dep. Variable: Wp R-squared: 0.987
Model: IV2SLS Adj. R-squared: 0.985
Method: Two Stage F-statistic: 424.2
Least Squares Prob (F-statistic): 3.57e-16
Date: Thu, 21 Jul 2022
Time: 00:33:21
No. Observations: 21
Df Residuals: 17
Df Model: 3
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
interc 1.5003 1.276 1.176 0.256 -1.191 4.192
X 0.4389 0.040 11.082 0.000 0.355 0.522
X1 0.1467 0.043 3.398 0.003 0.056 0.238
A 0.1304 0.032 4.026 0.001 0.062 0.199
==============================================================================
Omnibus: 0.449 Durbin-Watson: 1.963
Prob(Omnibus): 0.799 Jarque-Bera (JB): 0.545
Skew: 0.022 Prob(JB): 0.761
Kurtosis: 2.212 Cond. No. 641.
==============================================================================
Mismo modelo, pero usando fórmulas de statsmodels, etapa por etapa#
import statsmodels.formula.api as smf
rhs = ' + '.join(exogenas+predeterminadas)
klein_stage1 = klein.copy()
for y in endogenas:
klein_stage1[y] = smf.ols(f'{y} ~ {rhs}', data=klein).fit().fittedvalues
klein_stage1.eval('W=Wp+Wg', inplace=True)
regresores_eqs = ['P + P1 + W',
'P + P1 + K1',
'X + X1 + A']
for xx, yy in zip(regresores_eqs, endogenas[:3]):
print(f'\nRegresión para {yy}\n')
print(smf.ols(f'{yy} ~ {xx}', data=klein_stage1).fit().params)
Regresión para C
Intercept 16.554756
P 0.017302
P1 0.216234
W 0.810183
dtype: float64
Regresión para I
Intercept 20.278209
P 0.150222
P1 0.615944
K1 -0.157788
dtype: float64
Regresión para Wp
Intercept 1.500297
X 0.438859
X1 0.146674
A 0.130396
dtype: float64