Las pruebas de Box-Pierce y Ljung-Box.
Contents
1.6. Las pruebas de Box-Pierce y Ljung-Box.#
Cargar paquetes necesarios#
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats.distributions import chi2
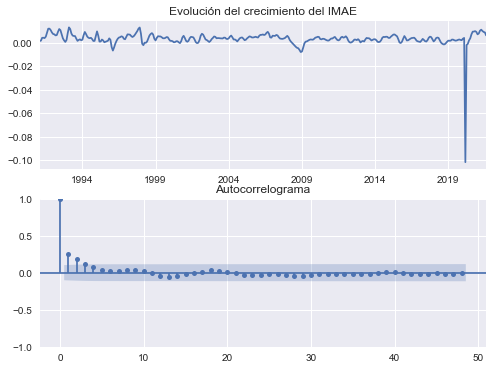
EJEMPLO 1: Crecimiento del IMAE de Costa Rica, serie tendencia-ciclo#
¿Es es crecimiento mensual del IMAE tendencia-ciclo un proceso ruido blanco?
log_imae = pd.read_csv("https://github.com/randall-romero/econometria/raw/master/data/log_imae.csv")
log_imae.index = pd.period_range(start='1991-01', freq='M', periods=log_imae.shape[0])
log_imae
| fecha | Original | Tendencia_ciclo | |
|---|---|---|---|
| 1991-01 | 1991-01-31 | 3.543337 | 3.436627 |
| 1991-02 | 1991-02-28 | 3.444160 | 3.438203 |
| 1991-03 | 1991-03-31 | 3.389929 | 3.439999 |
| 1991-04 | 1991-04-30 | 3.391805 | 3.444238 |
| 1991-05 | 1991-05-31 | 3.406380 | 3.448570 |
| ... | ... | ... | ... |
| 2021-04 | 2021-04-30 | 4.628316 | 4.657012 |
| 2021-05 | 2021-05-31 | 4.657245 | 4.667075 |
| 2021-06 | 2021-06-30 | 4.660920 | 4.676299 |
| 2021-07 | 2021-07-31 | 4.682706 | 4.685173 |
| 2021-08 | 2021-08-31 | 4.659956 | 4.691523 |
368 rows × 3 columns
growth = log_imae['Tendencia_ciclo'].diff().dropna()
T = growth.size # número de datos
M = 7 # máximo número de rezagos
rezagos = np.arange(1, M+1)
alpha = 0.05 # significancia de los test
Calculamos las autocovarianzas, a partir de un rezago
rho = sm.tsa.acf(growth, fft=True, nlags=M)[1:]
Calculamos el estadístico de Box-Pierce, para todos los rezagos desde el 1 hasta el 7
Qstar = T * (rho ** 2).cumsum()
Calculamos el estadístico de Ljung-Box
Q = T * (T+2) * ((rho ** 2)/(T-rezagos)).cumsum()
Calculamos los valores críticos, tomando en cuenta que \(k=0\) porque los datos que estamos usando no son residuos
vcrits = np.array([chi2(k).ppf(1-alpha) for k in rezagos])
Con carácter informativo nada más, calculamos la autocorrelación parcial
rhop = sm.tsa.pacf(growth, nlags=M, method='ols')[1:]
Juntamos todos los resultados en una tabla de resumen.
resumen = pd.DataFrame({'AC':rho, 'PAC': rhop, 'Box-Pierce':Qstar, 'Ljung-Box':Q, f'$\chi^2(m-k)$': vcrits}, index=rezagos)
resumen.index.name = 'Rezagos'
resumen.round(3)
| AC | PAC | Box-Pierce | Ljung-Box | $\chi^2(m-k)$ | |
|---|---|---|---|---|---|
| Rezagos | |||||
| 1 | 0.246 | 0.246 | 22.150 | 22.331 | 3.841 |
| 2 | 0.178 | 0.126 | 33.829 | 34.139 | 5.991 |
| 3 | 0.117 | 0.052 | 38.845 | 39.223 | 7.815 |
| 4 | 0.075 | 0.020 | 40.893 | 41.306 | 9.488 |
| 5 | 0.035 | -0.006 | 41.350 | 41.771 | 11.070 |
| 6 | 0.021 | -0.002 | 41.510 | 41.935 | 12.592 |
| 7 | 0.029 | 0.019 | 41.822 | 42.255 | 14.067 |
Graficamos los datos y el autocorrelograma
fig, axs = plt.subplots(2,1, figsize=[8,6])
growth.plot(ax=axs[0], title='Evolución del crecimiento del IMAE')
sm.graphics.tsa.plot_acf(growth, ax=axs[1], lags=48, alpha=0.05, title='Autocorrelograma');
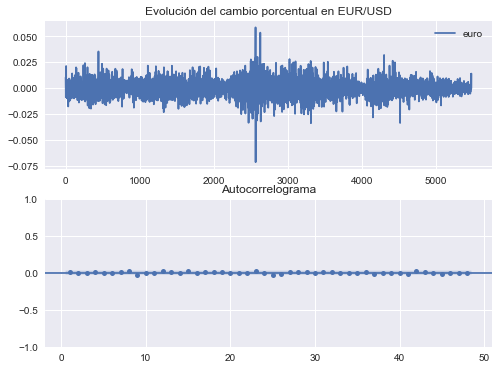
EJEMPLO 2: Crecimiento del tipo de cambio Euro/USD#
¿Es es crecimiento diario del tipo de cambio euro-dólar un proceso ruido blanco?
euro = pd.read_csv("https://github.com/randall-romero/econometria/raw/master/data/euro.csv")
#euro.index = pd.to_datetime(euro['fecha'])
euro.drop('fecha',inplace=True,axis=1)
depreciacion = euro.diff().dropna()
T = depreciacion.shape[0] # número de datos
M = 7 # máximo número de rezagos
rezagos = np.arange(1, M+1)
alpha = 0.05 # significancia de los test
Calculamos las autocovarianzas, a partir de un rezago
rho = sm.tsa.acf(depreciacion, fft=True, nlags=M)[1:]
Calculamos el estadístico de Box-Pierce, para todos los rezagos desde el 1 hasta el 7
Qstar = T * (rho ** 2).cumsum()
Calculamos el estadístico de Ljung-Box
Q = T * (T+2) * ((rho ** 2)/(T-rezagos)).cumsum()
Calculamos los valores críticos, tomando en cuenta que \(k=0\) porque los datos que estamos usando no son residuos
vcrits = np.array([chi2(k).ppf(1-alpha) for k in rezagos])
Con carácter informativo nada más, calculamos la autocorrelación parcial
rhop = sm.tsa.pacf(depreciacion, nlags=M, method='ols')[1:]
Juntamos todos los resultados en una tabla de resumen.
resumen = pd.DataFrame({'AC':rho, 'PAC': rhop, 'Box-Pierce':Qstar, 'Ljung-Box':Q, f'$\chi^2(m-k)$': vcrits}, index=rezagos)
resumen.index.name = 'Rezagos'
resumen.round(4)
| AC | PAC | Box-Pierce | Ljung-Box | $\chi^2(m-k)$ | |
|---|---|---|---|---|---|
| Rezagos | |||||
| 1 | 0.0042 | 0.0042 | 0.0948 | 0.0949 | 3.8415 |
| 2 | -0.0063 | -0.0064 | 0.3144 | 0.3146 | 5.9915 |
| 3 | 0.0001 | 0.0002 | 0.3145 | 0.3147 | 7.8147 |
| 4 | 0.0082 | 0.0082 | 0.6825 | 0.6831 | 9.4877 |
| 5 | 0.0022 | 0.0021 | 0.7082 | 0.7088 | 11.0705 |
| 6 | -0.0076 | -0.0076 | 1.0282 | 1.0293 | 12.5916 |
| 7 | 0.0106 | 0.0108 | 1.6485 | 1.6507 | 14.0671 |
Graficamos los datos y el autocorrelograma
fig, axs = plt.subplots(2,1, figsize=[8,6])
depreciacion.plot(ax=axs[0], title='Evolución del cambio porcentual en EUR/USD')
sm.graphics.tsa.plot_acf(depreciacion, zero=False, ax=axs[1], lags=48, alpha=0.05, title='Autocorrelograma');