4.4. Detectando raíces unitarias#

La prueba Dickey-Fuller#

Caminata aleatoria como serie AR(1)

El modelo más sencillo de una serie con raíz unitaria, la caminata aleatoria, es un proceso AR(1)

\[\begin{equation*} y_t = \phi y_{t-1} + \epsilon_t \end{equation*}\]

en el cual se cumple que \(\phi=1\).

Entonces resulta natural, para determinar si una serie es una caminata aleatoria, estimar esta ecuación y comprobar la hipótesis \(\phi=1\).

Alternativamente, restando \(y_{t-1}\) de ambos lados podemos estimar

\[\begin{align*} y_t - y_{t-1} &= (\phi-1) y_{t-1} + \epsilon_t \\ \Delta y_t &= \gamma y_{t-1} + \epsilon_t \end{align*}\]

y comprobar si

\[\begin{align*} H_0:\quad \gamma_0 &= 0 \qquad \text{versus} & H_1:\quad \gamma_0 &<0 \end{align*}\]

No obstante, Dickey y Fuller (1979) encontraron que si la hipótesis nula es verdadera, la regresión anterior tiene series no estacionarias en ambos lados de la ecuación, por lo que no se cumple que

\[\begin{equation*} z = \frac{\hat{\gamma}}{s.e.(\gamma)} \end{equation*}\]

tenga una distribución \(t\)-Student.

Para determinar la distribución de este estadístico, de manera que pueda realizarse la prueba de hipótesis, Dickey y Fuller realizaron experimentos de Monte Carlo, en los cuales

Se simula una caminata aleatoria con un tamaño de muestra predeterminado.
Se estima el modelo AR(1)
Se calcula el valor de \(z\)

Realizando muchas simulaciones como la anterior es posible aproximar la verdadera distribución del estadístico \(z\) bajo la hipótesis nula \(\gamma=0\).

Las pruebas de Dickey-Fuller

¿Tiene la serie \(y_t\) una raíz unitaria?

\[\begin{equation*} \qquad \left.\begin{aligned} \Delta y_t &= \phantom{a_0 + b_0 t +} \alert{\gamma} y_{t-1} + \epsilon_t \\ \Delta y_t &= a_0 + \phantom{b_0 t +} \alert{\gamma} y_{t-1} + \epsilon_t \\ \Delta y_t &= a_0 + b_0 t + \alert{\gamma} y_{t-1} + \epsilon_t \end{aligned}\right\} \alert{\gamma = 0} \end{equation*}\]

Estimar \(z = \frac{\hat{\gamma}}{s.e.(\gamma)}\) por mínimos cuadrados.

Si \(z\) es menor que el valor crítico de Dickey Fuller, entonces \(\gamma<0\), es decir, no hay raíz unitaria.

La distribución de Dickey-Fuller#

Ejemplo: Pruebas Dickey-Fuller

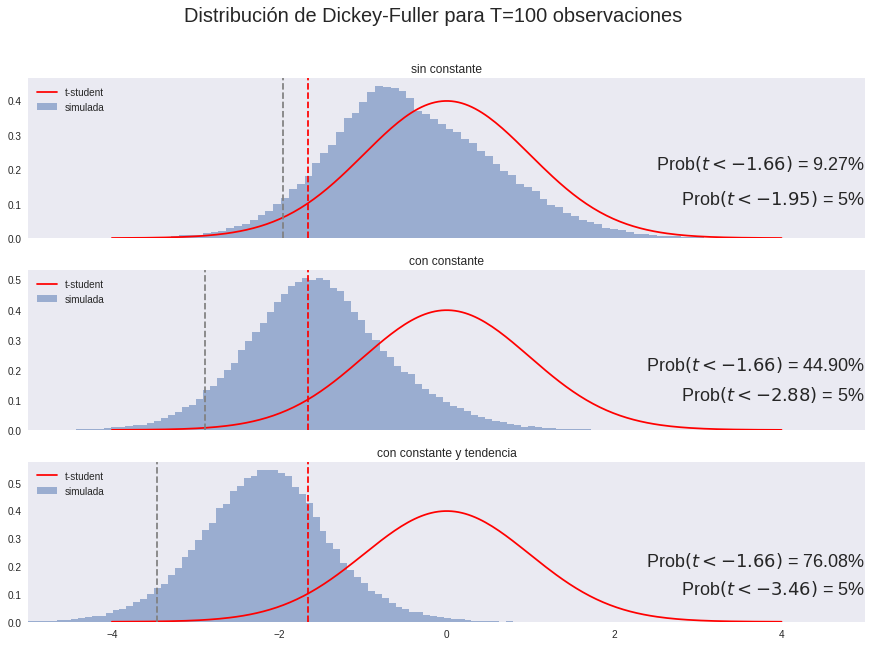
Al estimar por mínimos cuadrados ordinarios la regresión

\[\begin{equation*} \Delta\log\text{PIB}_t = c + \phi\log\text{PIB}_{t-1} + \epsilon_{t} \end{equation*}\]

encontramos

pib = bccr.SW(PIB=33783)
pib['lPIB'] = np.log(pib['PIB'])
pib['ΔlPIB'] = pib['lPIB'].diff()
pib['LlPIB'] = pib['lPIB'].shift()

res = smf.ols("ΔlPIB ~ LlPIB", data=pib).fit()
res.summary().tables[1]

Los resultados de la tabla indican que \(\phi\) es significativamente distinto de cero al 5% de significancia, pero este resultado es incorrecto porque en esta regresión el estadístico \(t\) no tiene la distribución \(t\)-Student.

Además, la prueba reportada es de dos colas, mientras que la apropiada es de una cola.

Por ello, recurrimos a los valores críticos de Dickey-Fuller

tabla_dickey_fuller(pib['lPIB'], DF, diff=0, specs=['c'])

Por otra parte, si realizamos las pruebas de Dickey-Fuller a la primera diferencia del (logaritmo del) PIB trimestral encontramos

pib['Δ2lPIB'] = pib['ΔlPIB'].diff()
pib['LΔlPIB'] = pib['ΔlPIB'].shift()

res = smf.ols("Δ2lPIB ~ LΔlPIB", data=pib).fit()
res.summary().tables[1]

tabla_dickey_fuller(pib['ΔlPIB'], DF, diff=0, specs=['c'])

Como en todos los casos el valor \(z\) estimado es menor que el valor crítico de Dickey-Fuller (sin importar cuál nivel de significancia utilizamos), concluimos que el crecimiento trimestral del PIB es estacionario (no tiene raíz unitaria).

Dado que no pudimos rechazar que el PIB tuviese raíz unitaria, pero sí lo hicimos para su primer diferencia, concluimos que el PIB es una serie I(1).

¿Qué hubiera pasado si en vez de diferenciar la serie, le extraemos una tendencia lineal?

Obtenemos los residuos de la regresión

\[\begin{equation*} \log\text{PIB}_t = c + at + \epsilon_{t} \end{equation*}\]

pib['t'] = np.arange(pib.shape[0])

res = smf.ols("lPIB ~ t", data=pib).fit()
res.summary().tables[1]

df = pd.concat([pib['lPIB'], res.fittedvalues, res.resid], axis=1)
df.columns = ["PIB", "Ajuste", "Residuos"]
df.index = df.index.to_timestamp() # para poder graficar con plotly

df[["PIB", "Ajuste"]].plot(title="PIB con tendencia lineal ajustada")

df[["Residuos"]].plot(title="Residuos")

Al aplicar las pruebas de Dickey-Fuller a los residuos, vemos que

tabla_dickey_fuller(res.resid, DF)

Ninguna de las pruebas rechaza la presencia de una raíz unitaria.

La prueba aumentada de Dickey-Fuller#

Caminata aleatoria como serie AR(p)

No todas las series de tiempo pueden representarse apropiadamente como un proceso AR(1).

La prueba de Dickey-Fuller puede aplicarse en estos casos también, aunque con modificaciones.

Consideremos por ejemplo un proceso AR(2):

\[\begin{align*} y_t &= \phi_1 y_{t-1} + \phi_2 y_{t-2} + \epsilon_t \\ &= \alert{(\phi_1 + \phi_2-1)}y_{t-1} - \alert{\phi_2y_{t-1} + y_{t-1}} +\phi_2 y_{t-2} + \epsilon_t \\ y_t - y_{t-1} &= (\phi_1 + \phi_2-1)y_{t-1} - \phi_2\left(y_{t-1} - y_{t-2}\right) + \epsilon_t \\ \Delta y_t &= (\phi_1 + \phi_2-1)y_{t-1} - \phi_2\Delta y_{t-1} + \epsilon_t \\ \Delta y_t &= \gamma y_{t-1} + a_1\Delta y_{t-1} + \epsilon_t \end{align*}\]

Esta serie tiene raíz unitaria si \(\gamma=0\).

Para permitir la posibilidad que la serie original sea AR(p+1), la prueba aumentada de Dickey-Fuller introduce \(p\) rezagos de la variable dependiente en la regresión original:

\[\begin{align*} \Delta y_t &= \phantom{a_0 + b_0 t +}\alert{\gamma} y_{t-1} + a_1\Delta y_{t-1} +\dots + a_p\Delta y_{t-p} + \epsilon_t \\ \Delta y_t &= a_0 \phantom{ + b_0 t } + \alert{\gamma} y_{t-1} + a_1\Delta y_{t-1} +\dots + a_p\Delta y_{t-p} + \epsilon_t \\ \Delta y_t &= a_0 + b_0 t + \alert{\gamma} y_{t-1} + a_1\Delta y_{t-1} +\dots + a_p\Delta y_{t-p} + \epsilon_t \end{align*}\]

En cualquiera de las formulaciones, la hipótesis nula es \(\gamma=0\).

Se utilizan los mismos valores críticos de la prueba de Dickey-Fuller.

Ejemplo: Pruebas aumentada de Dickey-Fuller

Al realizar las pruebas aumentadas de Dickey-Fuller del (logaritmo del) PIB trimestral de Costa Rica encontramos

tabla_dickey_fuller(pib['lPIB'], ADF, diff=0)

Esto confirma lo que ya habíamos encontrado: no podemos rechazar la hipótesis de que el PIB tenga raíz unitaria. En todos los casos, el número de rezagos corresponde al máximo rezago significativo.

Por otra parte, si realizamos las pruebas de Dickey-Fuller a la primera diferencia del (logaritmo del) PIB trimestral encontramos

tabla_dickey_fuller(pib['lPIB'], ADF, diff=1)

De nuevo concluimos que el crecimiento trimestral del PIB es estacionario (no tiene raíz unitaria).

Interpretando una prueba de Dickey Fuller#

Important

En la prueba DF, no rechazar la hipótesis de que una serie tenga raíz unitaria…

no implica que la serie sí tenga tal raíz unitaria.
solamente decimos que no hay evidencia suficiente para descartarla con un nivel “razonable” de significancia.

Esto es así porque bien podría ser el caso de que el verdadero valor de \(\phi\) sea ligeramente menor a uno (en cuyo caso el proceso AR(1) es estacionario), pero la prueba Dickey-Fuller no puede distinguirlo efectivamente de 1.

Potencia de la distribución de Dickey-Fuller#

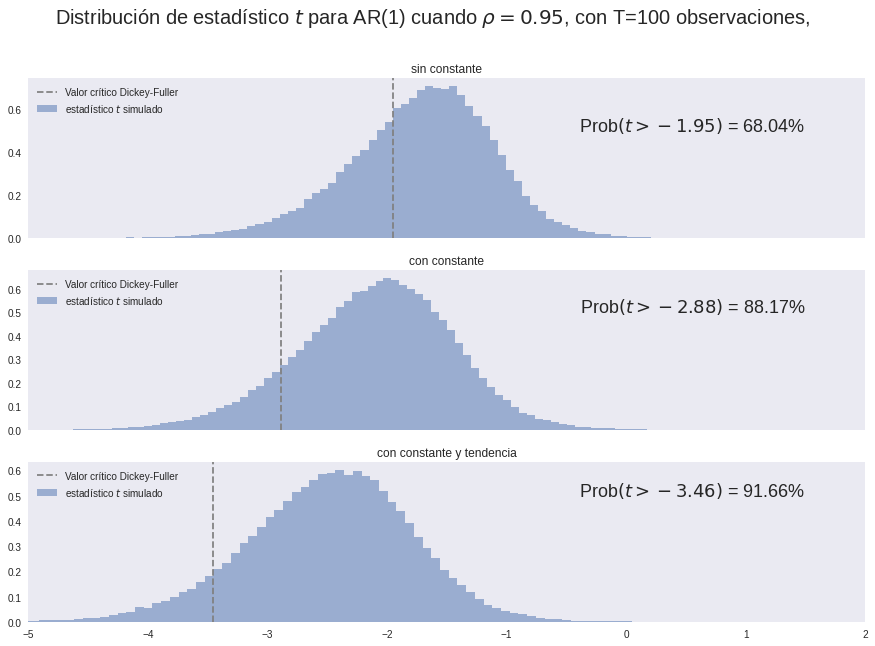
Limitaciones de las pruebas de raíz unitaria#

Hemos visto que la prueba de Dickey-Fuller tienen muy poca potencia para casos en que el proceso es persistente pero no integrado. Esto es una limitación también de otras pruebas de raíz unitaria, como la de Phillips-Perron.

Por ello, cuando se estudian series macroeconómicas con estos tests, usualmente se encuentra que tienen raíces unitarias.

Esto se debe a que la hipótesis nula es que sí hay raíz unitaria, y esta hipótesis solamente se rechaza cuando existe fuerte evidencia en su contra.

La prueba KPSS#

Kwiatkowski, Phillips, Schmidt y Shin (1992) proponen una prueba de estacionariedad: la hipótesis nula es que la serie es estacionaria.

Para ello, asumen que una serie puede ser expresada como la suma de una tendencia determinística, una caminata aleatoria, y un error estacionario (no necesariamente ruido blanco):

\[\begin{equation*} y_t = \notation{\xi t}{tendencia} + \notation{r_t}{caminata} + \notation{\omega_t}{estacionario} \end{equation*}\]

donde \(r_t\) es una caminata aleatoria

\[\begin{equation*} r_t = r_{t-1} + u_t, \qquad u_t\sim N(0, \sigma^2_u) \end{equation*}\]

La hipótesis de estacionariedad es simplemente \(\sigma^2_u = 0\).

Bajo la hipótesis nula, \(r_t = r_{t-1} = \dots = r_0\) una constante, por lo que la serie sería estacionaria alrededor de una tendencia:

\[\begin{equation*} y_t = r_0 + \xi t + \omega_t \end{equation*}\]

KPSS también consideran el caso particular en el que \(\xi=0\), es decir, la serie es simplemente estacionaria.

\[\begin{equation*} y_t = r_0 + \omega_t \end{equation*}\]

En cualquiera de estos dos casos, si \(e_1, e_2,\dots,e_T\) son los residuos de la regresión, se define

\[\begin{align*} S_t &= \sum_{i=1}^t e_i,\quad t=1,2,\dots,T \tag{suma parcial de residuos}\\ \hat{\sigma}^2_e &= \frac{1}{T}\sum_{t=1}^Te_t^2 \tag{varianza estimada del error} \end{align*}\]

\(\hat{\sigma}^2_e\) es un estimador consistente de la varianza de la parte estacionaria \(\omega_t\) solo si es ruido blanco.

Pero en la práctica, las series económicas rara vez cumplen esa restricción, por lo que KPSS proponen esta corrección para tomar en cuenta la posible correlación de \(\omega_t\):

\[\begin{equation*} s^2(l) = \frac{1}{T}\sum_{t=1}^Te_t^2 +\frac{2}{T}\sum_{s=1}^{l}\left[ \left(1-\tfrac{s}{1+l}\right)\sum_{t=s+1}^{T}e_{t}e_{t-s} \right] \end{equation*}\]

Así, para hacer una prueba KPSS hay que decidir:

si incluir o no la tendencia determinística
cuántos rezagos \(l\) incluir en la estimación de la varianza \(s^2(l)\)

La prueba KPSS

¿Es la serie \(y_t\)

\[\begin{align*} y_t &= \xi t + r_t + \omega_t \\ r_t &= r_{t-1} + u_t, \qquad u_t\sim N(0, \sigma^2_u) \\ \alert{\sigma^2_u} &\alert{=0} \end{align*}\]

\[\begin{equation*} LM = \sum_{t=1}^{T}\frac{S^2_t}{s^2(l)} \end{equation*}\]

Si \(LM\) es mayor que el valor crítico, rechazar la hipótesis nula y concluir que la serie tiene raíz unitaria.

KPSS proporcionan los siguientes valores críticos asintóticos, los cuales obtuvieron por simulación 50~000 iteraciones con muestras de 2000 datos.

Las pruebas son de una cola: se rechaza la hipótesis nula (de que la serie es estacionaria) cuando el estadístico LM es mayor al valor crítico seleccionado.

Ejemplo: Pruebas KPSS

Al realizar las pruebas KPSS del (logaritmo del) PIB trimestral de Costa Rica encontramos

result = pd.concat([tabla_KPSS(diff=r) for r in range(2)],
    axis=1,
    keys=['nivel','diferencia'])

result

Valores críticos

critical

En todas las especificaciones, podemos rechazar al 1% que el PIB sea estacionario.

Al 5%, en ningún caso podemos rechazar que el crecimiento del PIB (diferencia del logaritomo) sea estacionaria.

Juntos, estos resultados señalan que el PIB es un proceso I(1).

Ahora un ejemplo con datos de Estados Unidos.

Ejemplo: Raíces unitarias en series macroeconómicas de Estados Unidos

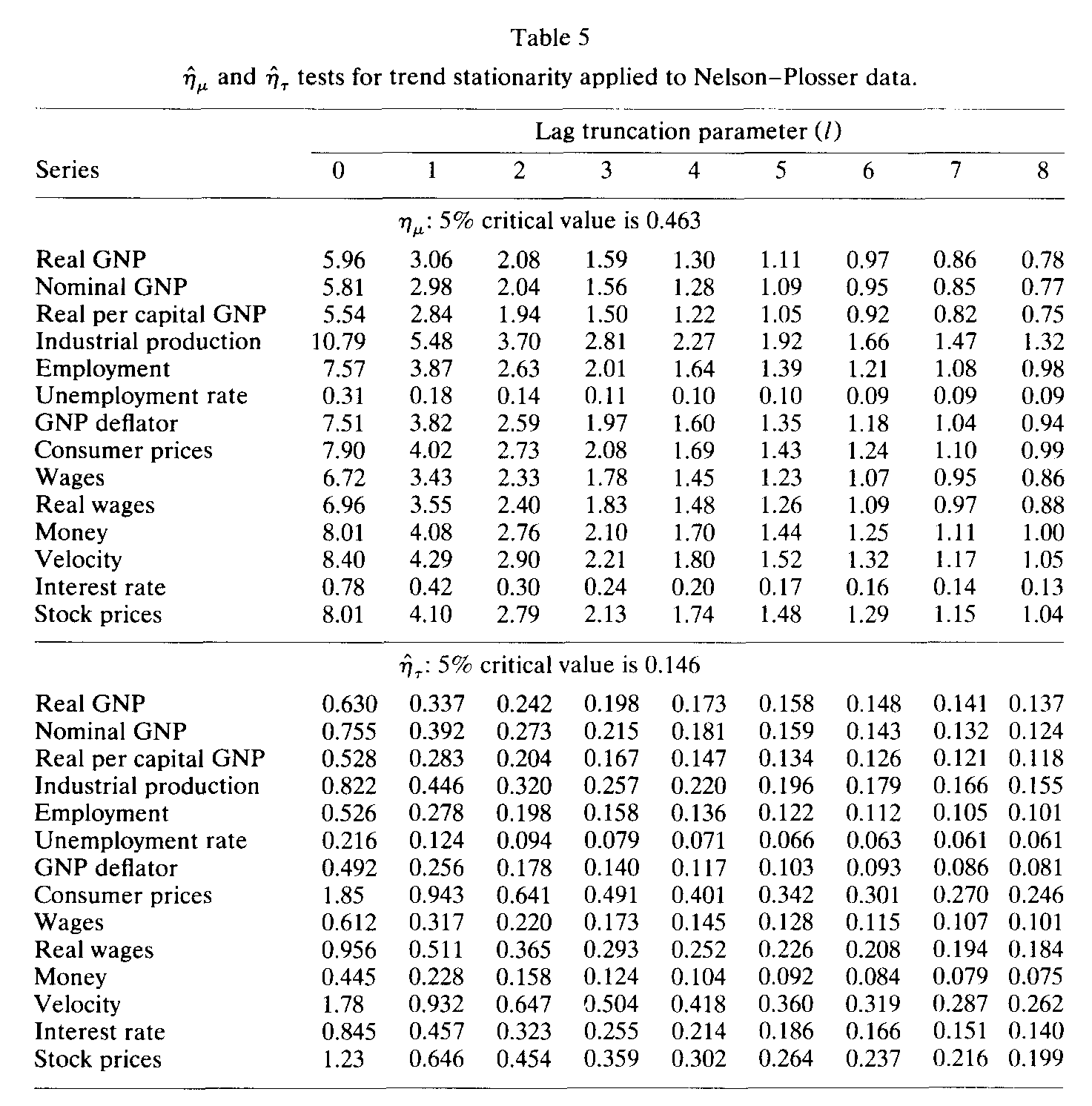
En uno de los artículos más citados en macroeconomía, Nelson y Plosser (1982) examinaron varias series macro de uso común, averiguando si tenían raíces unitarias.

Aplicando la prueba aumentada de Dickey-Fuller, concluyeron que todas menos una de las series analizadas tenían raíz unitaria.

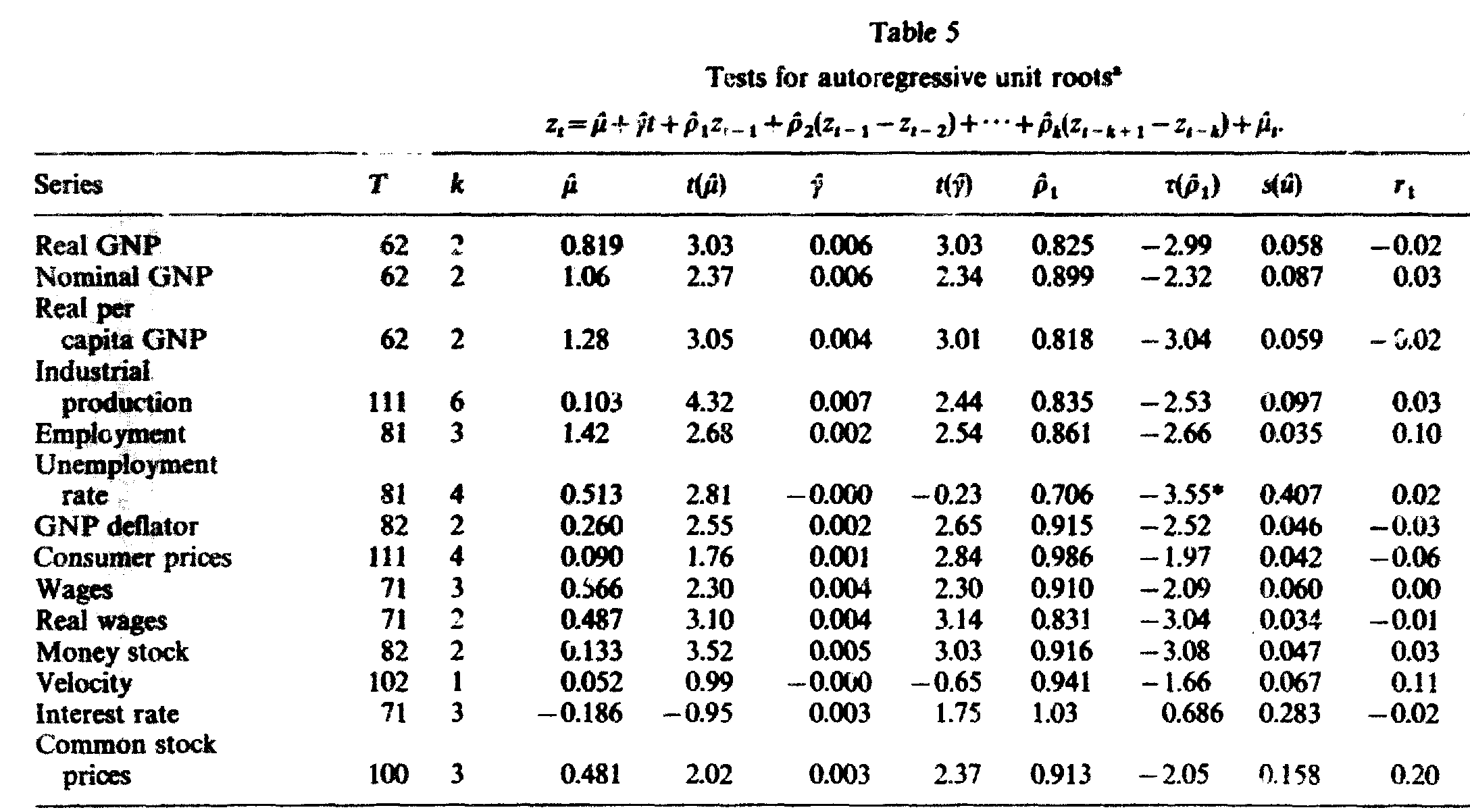
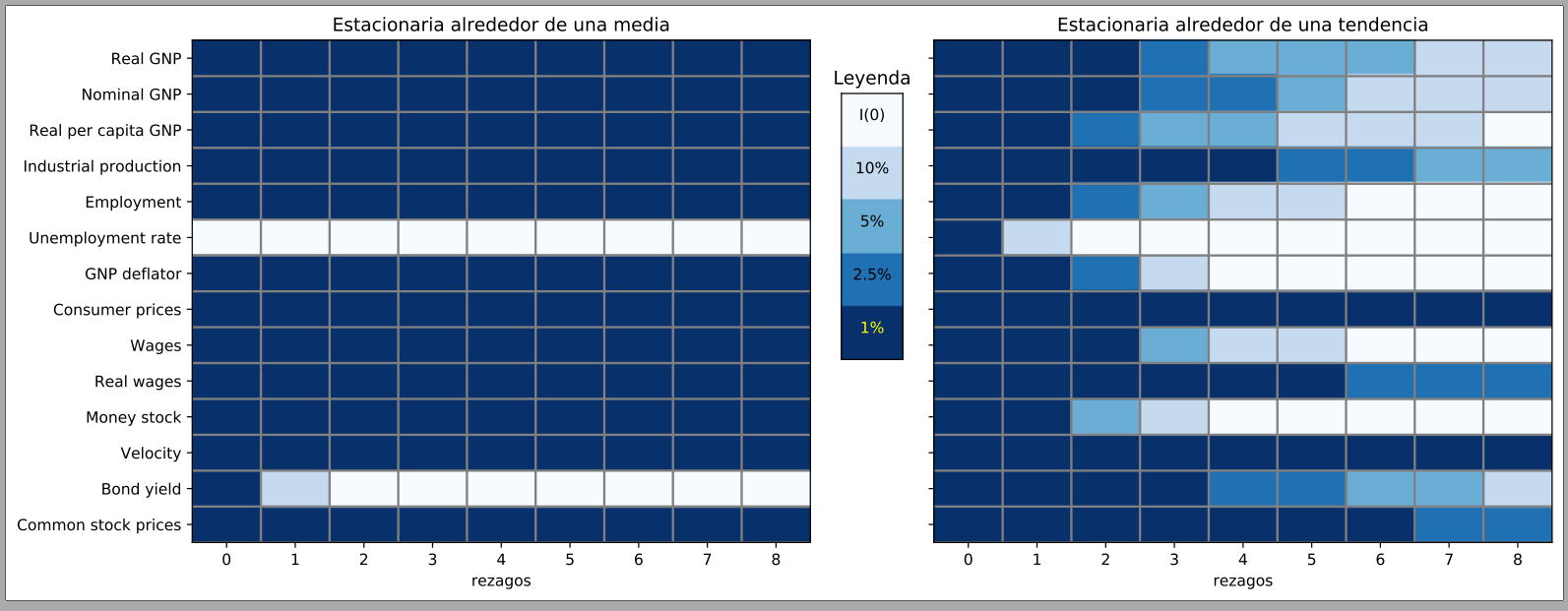
En su artículo original, KPSS aplican su prueba a las mismas series que utilizaron Nelson y Plosser.

Encontraron que para varias de las series no era posible rechazar la hipótesis de que fueran estacionarias alrededor de una tendencia.

Apuntes de Macroeconometría

Detectando raíces unitarias

Contents