4.4. Replicando el trabajo de Nelson y Plosser (1982)#

En un artículo muy citado

Nelson y Plosser 1982 Trends and Random Walks in Macroeconomic Time Series: Some evidence and implications. Journal of Monetary Economics 10, pp.139-162

los autores examinan varias series macroeconómicas de uso común.

Usando pruebas de Dickey-Fuller, encontraron que todas las series macroeconómicas contienen raíces unitarias, o más correctamente, que no podían rechazar la hipótesis nula de un raíz unitaria.

En esta parte del laboratorio replicamos algunos de los resultados de Nelson y Plosser.

Preparación#

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import acf, kpss
from statsmodels.formula.api import ols

Leer los datos y visualizarlos#

datos = pd.read_stata('https://github.com/randall-romero/econometria/raw/master/data/NelsonPlosserData.dta')
datos.set_index('year',inplace=True)
datos.index = datos.index.year

titulos = [f'r{i}' for i in range(1,7)] # para rotular unas tablas abajo

variables = {'lrgnp':'Real GNP',
           'lgnp':'Nominal GNP',
           'lpcrgnp':'Real per capita GNP',
           'lip':'Industrial production',
           'lemp':'Employment', 
           'lun':'Unemployment rate',
           'lprgnp':'GNP deflator',
           'lcpi':'Consumer prices',
           'lwg':'Wages',
           'lrwg':'Real wages', 
           'lm':'Money stock', 
           'lvel':'Velocity',
           'bnd':'Bond yield',
           'lsp500':'Common stock prices'}

datos = datos[variables.keys()].rename(columns=variables)
datos.plot(subplots=True, figsize=[15,15], layout=[-1,3]);

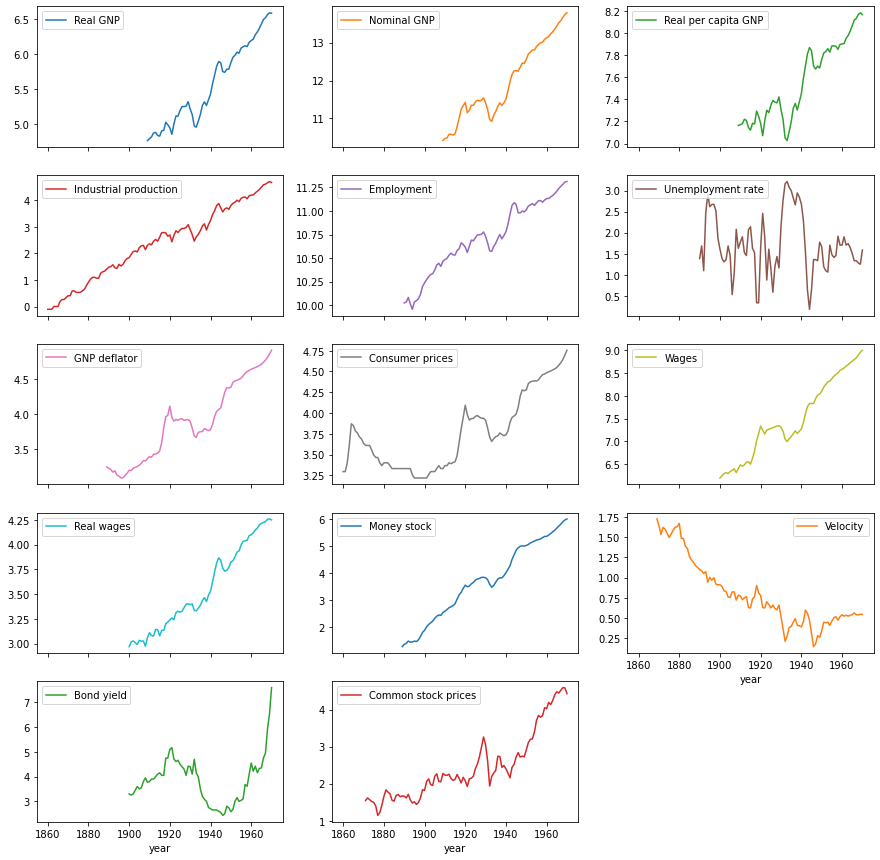
Calculando autocorrelaciones#

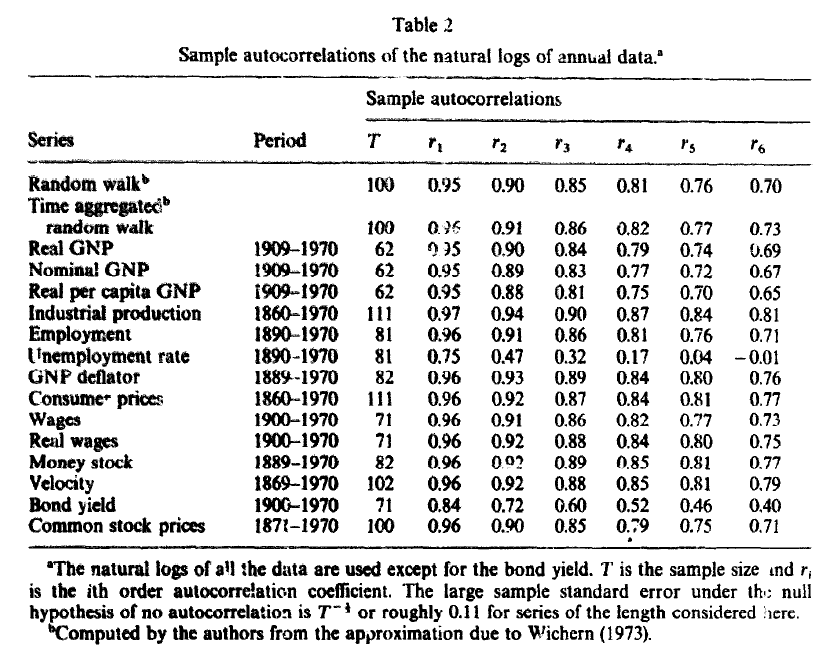
Nelson Plosser 1982 tabla 2

Fuente: Nelson y Plosser 1982 Trends and Random Walks in Macroeconomic Time Series: Some evidence and implications. Journal of Monetary Economics 10, pp.139-162

def acf6lags(nombre_variable, d):
    """
    Calcula los primeros 6 coeficientes de autocorrelación
    
    Args:
        nombre_variable: str, el nombre de una columna de la tabla "datos"
        d: número de veces que hay que diferenciar la serie (0 o 1 en la práctica)

    Returns:
        np.array, los 6 coeficientes de autocorrelación, redondeados a dos decimales
    """
    serie = datos[nombre_variable].diff(d) if d>0 else datos[nombre_variable]
    return acf(serie.dropna(), nlags=6, fft=False)[1:].round(2)

def tabla_acf(d):
    """
    Crea una tabla con las primeras 6 autocorrelaciones de todas las series en "datos"

    Args:
        d:  int, número de veces que hay que diferenciar la serie (0 o 1 en la práctica)

    Returns:
        una tabla de pandas, series en las filas, número de rezagos en las columnas
    """
    return pd.DataFrame([acf6lags(serie,d) for serie in datos], index=variables.values(), columns=titulos)

Serie en nivel#

tabla2 = tabla_acf(0)
tabla2

	r1	r2	r3	r4	r5	r6
Real GNP	0.95	0.90	0.84	0.79	0.74	0.69
Nominal GNP	0.95	0.89	0.83	0.77	0.72	0.67
Real per capita GNP	0.95	0.88	0.81	0.75	0.70	0.65
Industrial production	0.97	0.94	0.90	0.87	0.84	0.81
Employment	0.96	0.91	0.86	0.81	0.76	0.71
Unemployment rate	0.75	0.47	0.32	0.17	0.04	-0.01
GNP deflator	0.96	0.93	0.89	0.84	0.80	0.76
Consumer prices	0.96	0.92	0.87	0.84	0.80	0.77
Wages	0.96	0.91	0.86	0.82	0.77	0.73
Real wages	0.96	0.92	0.88	0.84	0.80	0.75
Money stock	0.96	0.92	0.89	0.85	0.81	0.77
Velocity	0.96	0.92	0.88	0.85	0.81	0.79
Bond yield	0.84	0.72	0.60	0.52	0.46	0.40
Common stock prices	0.96	0.90	0.85	0.79	0.75	0.71

def rango_datos(ser):
    """
    Determina el rango de los datos disponibles de una serie
    Args:
        ser: una serie de pandas

    Returns:
        str, primera observación -- última observación
    """
    return f'{ser.first_valid_index()} -- {ser.last_valid_index()}'

datos.apply(rango_datos)

Real GNP                 1909 -- 1970
Nominal GNP              1909 -- 1970
Real per capita GNP      1909 -- 1970
Industrial production    1860 -- 1970
Employment               1890 -- 1970
Unemployment rate        1890 -- 1970
GNP deflator             1889 -- 1970
Consumer prices          1860 -- 1970
Wages                    1900 -- 1970
Real wages               1900 -- 1970
Money stock              1889 -- 1970
Velocity                 1869 -- 1970
Bond yield               1900 -- 1970
Common stock prices      1871 -- 1970
dtype: object

tabla2.insert(0,'Period', datos.apply(rango_datos))
tabla2.insert(1, 'T', datos.apply(lambda ser: ser.dropna().count()))
tabla2

	Period	T	r1	r2	r3	r4	r5	r6
Real GNP	1909 -- 1970	62	0.95	0.90	0.84	0.79	0.74	0.69
Nominal GNP	1909 -- 1970	62	0.95	0.89	0.83	0.77	0.72	0.67
Real per capita GNP	1909 -- 1970	62	0.95	0.88	0.81	0.75	0.70	0.65
Industrial production	1860 -- 1970	111	0.97	0.94	0.90	0.87	0.84	0.81
Employment	1890 -- 1970	81	0.96	0.91	0.86	0.81	0.76	0.71
Unemployment rate	1890 -- 1970	81	0.75	0.47	0.32	0.17	0.04	-0.01
GNP deflator	1889 -- 1970	82	0.96	0.93	0.89	0.84	0.80	0.76
Consumer prices	1860 -- 1970	111	0.96	0.92	0.87	0.84	0.80	0.77
Wages	1900 -- 1970	71	0.96	0.91	0.86	0.82	0.77	0.73
Real wages	1900 -- 1970	71	0.96	0.92	0.88	0.84	0.80	0.75
Money stock	1889 -- 1970	82	0.96	0.92	0.89	0.85	0.81	0.77
Velocity	1869 -- 1970	102	0.96	0.92	0.88	0.85	0.81	0.79
Bond yield	1900 -- 1970	71	0.84	0.72	0.60	0.52	0.46	0.40
Common stock prices	1871 -- 1970	100	0.96	0.90	0.85	0.79	0.75	0.71

Serie en primera diferencia#

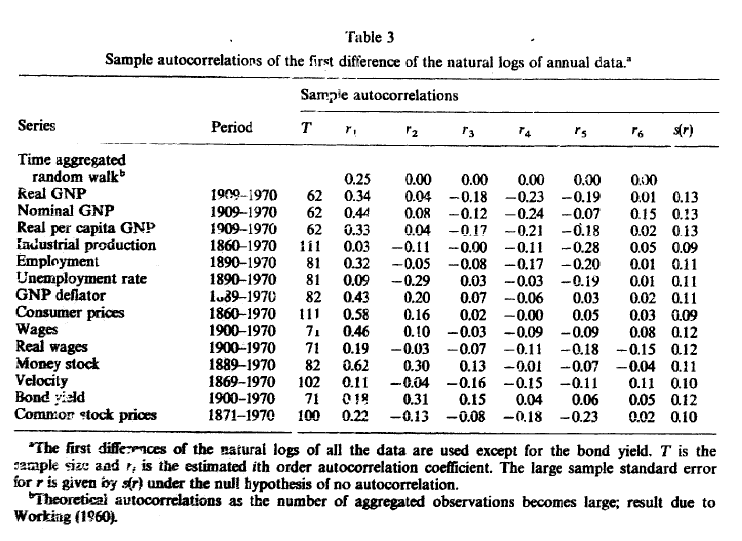
Nelson Plosser 1982 tabla 3

Fuente: Nelson y Plosser 1982 Trends and Random Walks in Macroeconomic Time Series: Some evidence and implications. Journal of Monetary Economics 10, pp.139-162

tabla3 = tabla_acf(1)
tabla3.insert(0,'Period', datos.apply(rango_datos))
tabla3.insert(1, 'T', datos.apply(lambda ser: ser.dropna().count()))
tabla3

	Period	T	r1	r2	r3	r4	r5	r6
Real GNP	1909 -- 1970	62	0.34	0.04	-0.18	-0.23	-0.19	0.01
Nominal GNP	1909 -- 1970	62	0.44	0.08	-0.12	-0.24	-0.07	0.15
Real per capita GNP	1909 -- 1970	62	0.33	0.04	-0.17	-0.21	-0.18	0.02
Industrial production	1860 -- 1970	111	0.03	-0.11	-0.00	-0.11	-0.28	0.05
Employment	1890 -- 1970	81	0.32	-0.05	-0.08	-0.17	-0.20	0.01
Unemployment rate	1890 -- 1970	81	0.09	-0.29	0.03	-0.03	-0.19	0.01
GNP deflator	1889 -- 1970	82	0.43	0.20	0.07	-0.06	0.03	0.02
Consumer prices	1860 -- 1970	111	0.58	0.16	0.02	-0.00	0.05	0.03
Wages	1900 -- 1970	71	0.46	0.10	-0.03	-0.09	-0.09	0.08
Real wages	1900 -- 1970	71	0.19	-0.03	-0.07	-0.11	-0.18	-0.15
Money stock	1889 -- 1970	82	0.62	0.30	0.13	-0.01	-0.07	-0.04
Velocity	1869 -- 1970	102	0.11	-0.04	-0.16	-0.15	-0.11	0.11
Bond yield	1900 -- 1970	71	0.18	0.31	0.15	0.04	0.06	0.05
Common stock prices	1871 -- 1970	100	0.22	-0.13	-0.08	-0.18	-0.23	0.02

Desviaciones respecto a una tendencia lineal#

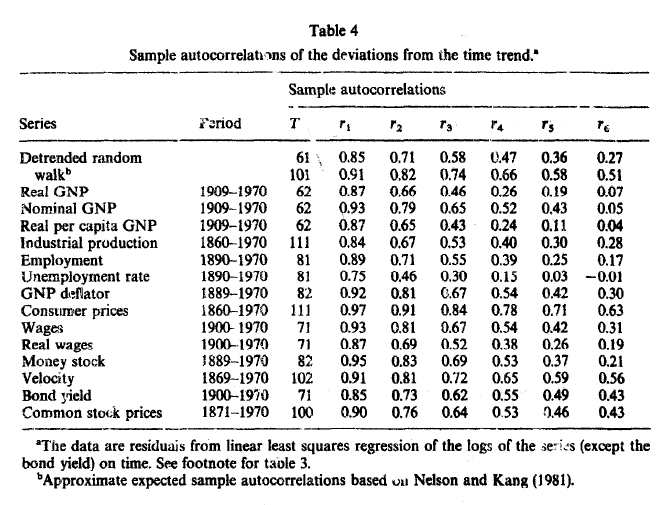
Nelson Plosser 1982 tabla 4

Fuente: Nelson y Plosser 1982 Trends and Random Walks in Macroeconomic Time Series: Some evidence and implications. Journal of Monetary Economics 10, pp.139-162

def acf_deviation_from_trend(nombre_variable):
    """
    Calcular las primeras 6 autocorrelaciones de la desviación de una serie respecto a 
    su tendencia lineal.
    
    Se estima por mínimos cuadrados ordinarios una regresión de la forma
        y = intercepto + time
    
    y se calcula la autocorrelación de los residuos.
    Args:
        nombre_variable: str, nombre de una variable de la tabla "datos" 

    Returns:
        np.array, los 6 coeficientes de autocorrelación, redondeados a dos decimales
    """
    temp = datos[[nombre_variable]].dropna()
    temp.columns = ['y']
    temp['t'] = np.arange(temp.shape[0]) 
    resid = ols('y ~ t', temp).fit().resid
    return acf(resid, nlags=6, fft=False)[1:].round(2)

tabla4 = pd.DataFrame([acf_deviation_from_trend(ser) for ser in datos], index=variables.values(), columns=titulos)
tabla4.insert(0,'Period', datos.apply(rango_datos))
tabla4.insert(1, 'T', datos.apply(lambda ser: ser.dropna().count()))
tabla4

	Period	T	r1	r2	r3	r4	r5	r6
Real GNP	1909 -- 1970	62	0.87	0.66	0.44	0.26	0.13	0.07
Nominal GNP	1909 -- 1970	62	0.93	0.79	0.65	0.52	0.43	0.35
Real per capita GNP	1909 -- 1970	62	0.87	0.65	0.43	0.24	0.11	0.04
Industrial production	1860 -- 1970	111	0.84	0.67	0.53	0.40	0.29	0.28
Employment	1890 -- 1970	81	0.89	0.71	0.55	0.39	0.25	0.17
Unemployment rate	1890 -- 1970	81	0.75	0.46	0.30	0.15	0.03	-0.01
GNP deflator	1889 -- 1970	82	0.92	0.81	0.67	0.54	0.42	0.30
Consumer prices	1860 -- 1970	111	0.97	0.91	0.84	0.78	0.71	0.63
Wages	1900 -- 1970	71	0.93	0.81	0.67	0.54	0.42	0.31
Real wages	1900 -- 1970	71	0.87	0.69	0.52	0.38	0.26	0.19
Money stock	1889 -- 1970	82	0.95	0.83	0.69	0.53	0.37	0.21
Velocity	1869 -- 1970	102	0.91	0.81	0.72	0.65	0.59	0.56
Bond yield	1900 -- 1970	71	0.85	0.73	0.62	0.55	0.49	0.43
Common stock prices	1871 -- 1970	100	0.90	0.76	0.64	0.53	0.46	0.43

Mostrar las tablas 2 a 4 en una sola#

pd.concat([tabla2, tabla3, tabla4], axis=1)

	Period	T	r1	r2	r3	r4	r5	r6	Period	T	...	r5	r6	Period	T	r1	r2	r3	r4	r5	r6
Real GNP	1909 -- 1970	62	0.95	0.90	0.84	0.79	0.74	0.69	1909 -- 1970	62	...	-0.19	0.01	1909 -- 1970	62	0.87	0.66	0.44	0.26	0.13	0.07
Nominal GNP	1909 -- 1970	62	0.95	0.89	0.83	0.77	0.72	0.67	1909 -- 1970	62	...	-0.07	0.15	1909 -- 1970	62	0.93	0.79	0.65	0.52	0.43	0.35
Real per capita GNP	1909 -- 1970	62	0.95	0.88	0.81	0.75	0.70	0.65	1909 -- 1970	62	...	-0.18	0.02	1909 -- 1970	62	0.87	0.65	0.43	0.24	0.11	0.04
Industrial production	1860 -- 1970	111	0.97	0.94	0.90	0.87	0.84	0.81	1860 -- 1970	111	...	-0.28	0.05	1860 -- 1970	111	0.84	0.67	0.53	0.40	0.29	0.28
Employment	1890 -- 1970	81	0.96	0.91	0.86	0.81	0.76	0.71	1890 -- 1970	81	...	-0.20	0.01	1890 -- 1970	81	0.89	0.71	0.55	0.39	0.25	0.17
Unemployment rate	1890 -- 1970	81	0.75	0.47	0.32	0.17	0.04	-0.01	1890 -- 1970	81	...	-0.19	0.01	1890 -- 1970	81	0.75	0.46	0.30	0.15	0.03	-0.01
GNP deflator	1889 -- 1970	82	0.96	0.93	0.89	0.84	0.80	0.76	1889 -- 1970	82	...	0.03	0.02	1889 -- 1970	82	0.92	0.81	0.67	0.54	0.42	0.30
Consumer prices	1860 -- 1970	111	0.96	0.92	0.87	0.84	0.80	0.77	1860 -- 1970	111	...	0.05	0.03	1860 -- 1970	111	0.97	0.91	0.84	0.78	0.71	0.63
Wages	1900 -- 1970	71	0.96	0.91	0.86	0.82	0.77	0.73	1900 -- 1970	71	...	-0.09	0.08	1900 -- 1970	71	0.93	0.81	0.67	0.54	0.42	0.31
Real wages	1900 -- 1970	71	0.96	0.92	0.88	0.84	0.80	0.75	1900 -- 1970	71	...	-0.18	-0.15	1900 -- 1970	71	0.87	0.69	0.52	0.38	0.26	0.19
Money stock	1889 -- 1970	82	0.96	0.92	0.89	0.85	0.81	0.77	1889 -- 1970	82	...	-0.07	-0.04	1889 -- 1970	82	0.95	0.83	0.69	0.53	0.37	0.21
Velocity	1869 -- 1970	102	0.96	0.92	0.88	0.85	0.81	0.79	1869 -- 1970	102	...	-0.11	0.11	1869 -- 1970	102	0.91	0.81	0.72	0.65	0.59	0.56
Bond yield	1900 -- 1970	71	0.84	0.72	0.60	0.52	0.46	0.40	1900 -- 1970	71	...	0.06	0.05	1900 -- 1970	71	0.85	0.73	0.62	0.55	0.49	0.43
Common stock prices	1871 -- 1970	100	0.96	0.90	0.85	0.79	0.75	0.71	1871 -- 1970	100	...	-0.23	0.02	1871 -- 1970	100	0.90	0.76	0.64	0.53	0.46	0.43

14 rows × 24 columns

pd.concat([tabla2, tabla3.iloc[:,-6:], tabla4.iloc[:,-6:]], axis=1, keys=['Niveles','Diferencias','Desviación de tendencia'])

	Niveles								Diferencias						Desviación de tendencia
	Period	T	r1	r2	r3	r4	r5	r6	r1	r2	r3	r4	r5	r6	r1	r2	r3	r4	r5	r6
Real GNP	1909 -- 1970	62	0.95	0.90	0.84	0.79	0.74	0.69	0.34	0.04	-0.18	-0.23	-0.19	0.01	0.87	0.66	0.44	0.26	0.13	0.07
Nominal GNP	1909 -- 1970	62	0.95	0.89	0.83	0.77	0.72	0.67	0.44	0.08	-0.12	-0.24	-0.07	0.15	0.93	0.79	0.65	0.52	0.43	0.35
Real per capita GNP	1909 -- 1970	62	0.95	0.88	0.81	0.75	0.70	0.65	0.33	0.04	-0.17	-0.21	-0.18	0.02	0.87	0.65	0.43	0.24	0.11	0.04
Industrial production	1860 -- 1970	111	0.97	0.94	0.90	0.87	0.84	0.81	0.03	-0.11	-0.00	-0.11	-0.28	0.05	0.84	0.67	0.53	0.40	0.29	0.28
Employment	1890 -- 1970	81	0.96	0.91	0.86	0.81	0.76	0.71	0.32	-0.05	-0.08	-0.17	-0.20	0.01	0.89	0.71	0.55	0.39	0.25	0.17
Unemployment rate	1890 -- 1970	81	0.75	0.47	0.32	0.17	0.04	-0.01	0.09	-0.29	0.03	-0.03	-0.19	0.01	0.75	0.46	0.30	0.15	0.03	-0.01
GNP deflator	1889 -- 1970	82	0.96	0.93	0.89	0.84	0.80	0.76	0.43	0.20	0.07	-0.06	0.03	0.02	0.92	0.81	0.67	0.54	0.42	0.30
Consumer prices	1860 -- 1970	111	0.96	0.92	0.87	0.84	0.80	0.77	0.58	0.16	0.02	-0.00	0.05	0.03	0.97	0.91	0.84	0.78	0.71	0.63
Wages	1900 -- 1970	71	0.96	0.91	0.86	0.82	0.77	0.73	0.46	0.10	-0.03	-0.09	-0.09	0.08	0.93	0.81	0.67	0.54	0.42	0.31
Real wages	1900 -- 1970	71	0.96	0.92	0.88	0.84	0.80	0.75	0.19	-0.03	-0.07	-0.11	-0.18	-0.15	0.87	0.69	0.52	0.38	0.26	0.19
Money stock	1889 -- 1970	82	0.96	0.92	0.89	0.85	0.81	0.77	0.62	0.30	0.13	-0.01	-0.07	-0.04	0.95	0.83	0.69	0.53	0.37	0.21
Velocity	1869 -- 1970	102	0.96	0.92	0.88	0.85	0.81	0.79	0.11	-0.04	-0.16	-0.15	-0.11	0.11	0.91	0.81	0.72	0.65	0.59	0.56
Bond yield	1900 -- 1970	71	0.84	0.72	0.60	0.52	0.46	0.40	0.18	0.31	0.15	0.04	0.06	0.05	0.85	0.73	0.62	0.55	0.49	0.43
Common stock prices	1871 -- 1970	100	0.96	0.90	0.85	0.79	0.75	0.71	0.22	-0.13	-0.08	-0.18	-0.23	0.02	0.90	0.76	0.64	0.53	0.46	0.43

Estimar la regresión Dickey-Fuller, “a pie”#

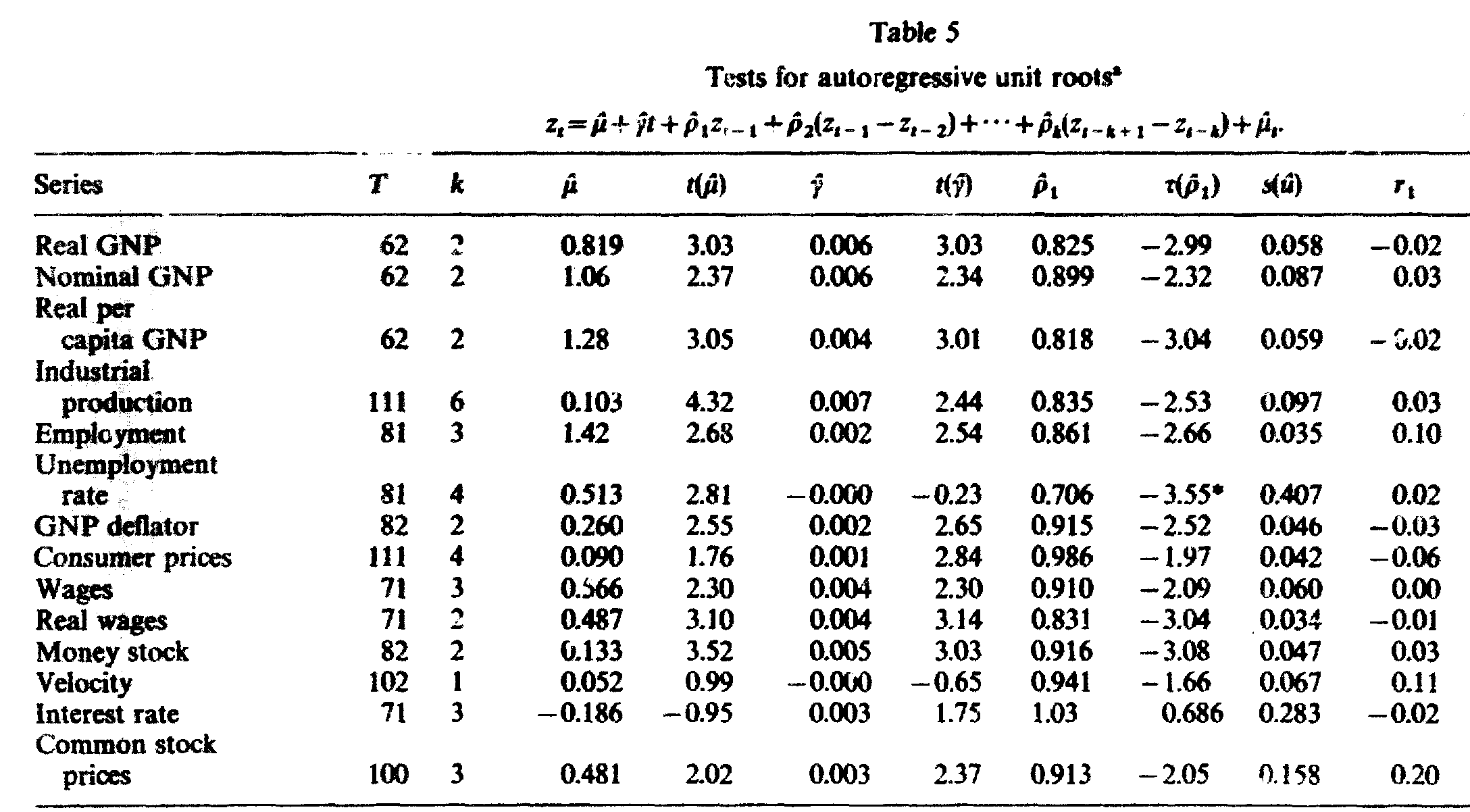
Nelson Plosser 1982 tabla 5

Fuente: Nelson y Plosser 1982 Trends and Random Walks in Macroeconomic Time Series: Some evidence and implications. Journal of Monetary Economics 10, pp.139-162

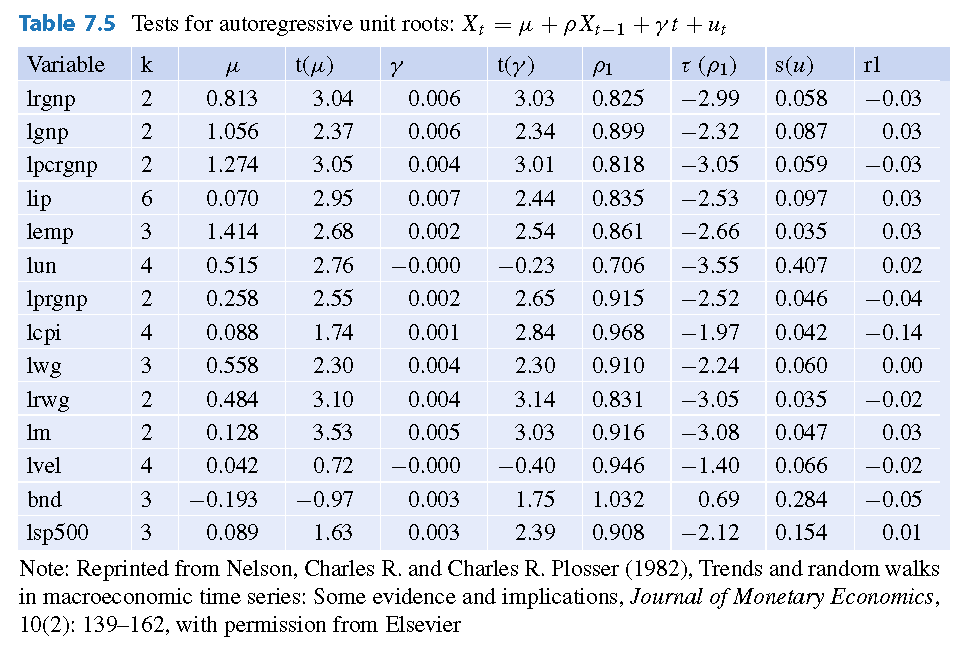
Levendis tabla 7.5

Fuente: Levendis 2018 Time Series Econometrics: Learning Through Replication. Springer

def ADFregression(nombre_variable, k):
    """
    Estima la regresión necesaria para la prueba aumentada de Dickey-Fuller
    Args:
        nombre_variable: str, nombre de una variable de la tabla "datos"
        k: Número de rezagos del proceso AR subyacente (1 + rezagos en regresión)

    Returns:
        Un objeto de resultados estimados de statsmodels
    """
    temp = datos[[nombre_variable]].dropna()
    temp.columns=['Y']
    temp['DY'] = temp['Y'].diff()
    temp['LY'] = temp['Y'].shift()
    temp['t'] = np.arange(temp.shape[0])    
    for j in range(1, k):
        temp[f'D{j}Y'] = temp['DY'].shift(j)
        regresores = ' + '.join(temp.columns[2:])
    print(regresores)
    frml = 'DY ~ ' + regresores
    return ols(frml, temp).fit()
    

ADFregression('Real GNP', 4).summary()

LY + t + D1Y + D2Y + D3Y

OLS Regression Results
Dep. Variable:	DY	R-squared:	0.265
Model:	OLS	Adj. R-squared:	0.194
Method:	Least Squares	F-statistic:	3.753
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	0.00563
Time:	00:34:55	Log-Likelihood:	84.601
No. Observations:	58	AIC:	-157.2
Df Residuals:	52	BIC:	-144.8
Df Model:	5
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	0.8645	0.317	2.723	0.009	0.227	1.501
LY	-0.1880	0.070	-2.687	0.010	-0.328	-0.048
t	0.0062	0.002	2.803	0.007	0.002	0.011
D1Y	0.3991	0.129	3.091	0.003	0.140	0.658
D2Y	0.0741	0.140	0.531	0.598	-0.206	0.354
D3Y	-0.0693	0.136	-0.509	0.613	-0.343	0.204

Omnibus:	3.110	Durbin-Watson:	2.010
Prob(Omnibus):	0.211	Jarque-Bera (JB):	2.243
Skew:	-0.313	Prob(JB):	0.326
Kurtosis:	3.732	Cond. No.	1.57e+03

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.57e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

def NelsonPlosser(ser, k):
    """
    Calcula varios estadísticos de la regresión de la prueba aumentada de Dickey-Fuller, 
    para reproducir los resultados reportados en la tabla 5 de Nelson y Plosser (1982)
    
    Args:
        ser: str, nombre abreviado de una variable de la tabla "datos"
        k: Número de rezagos del proceso AR subyacente (1 + rezagos en regresión)

    Returns:
        dict, estadísticos calculados        
    """
    nombre_variable = variables[ser]
    fuller5pct = -3.45
    model = ADFregression(nombre_variable, k)
    
    estadisticos = {
        'mu': np.round(model.params['Intercept'], 3),
        't(mu)': np.round(model.tvalues['Intercept'], 2),
        'gamma': np.round(model.params['t'], 3),
        't(gamma)': np.round(model.tvalues['t'], 2),
        'rho': np.round(model.params['LY'] + 1, 3),
        't(rho)': np.round(model.tvalues['LY'], 2),
        's(u)': np.round(np.sqrt(model.mse_resid),3),
        'r1': acf(model.resid, nlags=1, fft=False)[1].round(2),
        'resultado': '* estacionaria' if model.tvalues['LY'] < fuller5pct else 'raiz unitaria'
    }
    
    return estadisticos
    

NelsonPlosser('lrgnp', 3)

LY + t + D1Y + D2Y

{'mu': 0.872,
 't(mu)': 2.98,
 'gamma': 0.006,
 't(gamma)': 2.99,
 'rho': 0.811,
 't(rho)': -2.94,
 's(u)': 0.059,
 'r1': -0.01,
 'resultado': 'raiz unitaria'}

rezagos = {'lrgnp':2, 'lgnp':2, 'lpcrgnp':2,'lip':6, 'lemp':3, 'lun':4, 'lprgnp':2, 'lcpi':4, 'lwg':3, 'lrwg':2, 'lm':2, 'lvel':4,'bnd':3,'lsp500':3}

tabla5 = pd.DataFrame([NelsonPlosser(ser, lags) for ser, lags in rezagos.items()], index=rezagos.keys())
tabla5

LY + t + D1Y
LY + t + D1Y
LY + t + D1Y
LY + t + D1Y + D2Y + D3Y + D4Y + D5Y
LY + t + D1Y + D2Y
LY + t + D1Y + D2Y + D3Y

LY + t + D1Y
LY + t + D1Y + D2Y + D3Y

LY + t + D1Y + D2Y
LY + t + D1Y
LY + t + D1Y
LY + t + D1Y + D2Y + D3Y
LY + t + D1Y + D2Y
LY + t + D1Y + D2Y

	mu	t(mu)	gamma	t(gamma)	rho	t(rho)	s(u)	r1	resultado
lrgnp	0.813	3.04	0.006	3.03	0.825	-2.99	0.058	-0.03	raiz unitaria
lgnp	1.056	2.37	0.006	2.34	0.899	-2.32	0.087	0.03	raiz unitaria
lpcrgnp	1.274	3.05	0.004	3.01	0.818	-3.05	0.059	-0.03	raiz unitaria
lip	0.070	2.95	0.007	2.44	0.835	-2.53	0.097	0.03	raiz unitaria
lemp	1.414	2.68	0.002	2.54	0.861	-2.66	0.035	0.03	raiz unitaria
lun	0.515	2.76	-0.000	-0.23	0.706	-3.55	0.407	0.02	* estacionaria
lprgnp	0.258	2.55	0.002	2.65	0.915	-2.52	0.046	-0.04	raiz unitaria
lcpi	0.088	1.74	0.001	2.84	0.968	-1.97	0.042	-0.14	raiz unitaria
lwg	0.558	2.30	0.004	2.30	0.910	-2.24	0.060	0.00	raiz unitaria
lrwg	0.484	3.10	0.004	3.14	0.831	-3.05	0.035	-0.02	raiz unitaria
lm	0.128	3.53	0.005	3.03	0.916	-3.08	0.047	0.03	raiz unitaria
lvel	0.042	0.72	-0.000	-0.40	0.946	-1.40	0.066	-0.02	raiz unitaria
bnd	-0.193	-0.97	0.003	1.75	1.032	0.69	0.284	-0.05	raiz unitaria
lsp500	0.089	1.63	0.003	2.39	0.908	-2.12	0.154	0.01	raiz unitaria

NOTA: Una versión anterior de este archivo tenía la réplica del trabajo de KPSS. Ese código ahora está en el cuaderno KPSS.ipynb.

Apuntes de Macroeconometría

Replicando el trabajo de Nelson y Plosser (1982)

Contents