8.1. Simulación de un VAR(1)

Suponga el siguiente modelo dinámico

\[\begin{align*} x_t &= 4 + 0.8x_{t-1} + y_{t-1} + \epsilon_{x,t} \\ y_t &= 1 + 0.1x_{t-1} + 0.5y_{t-1} + \epsilon_{y,t} \end{align*}\]

que puede escribirse

\[\begin{equation*} \underset{X_t}{\begin{pmatrix}x_t \\ y_t\end{pmatrix}} = \underset{c}{\begin{pmatrix}0.9 \\ 1.8\end{pmatrix}} + \underset{A}{\begin{pmatrix}0.8 & 0.7 \\ -0.2 & 0.8\end{pmatrix}} \underset{X_{t-1}}{\begin{pmatrix}x_{t-1} \\ y_{t-1}\end{pmatrix}} + \underset{\epsilon_t}{\begin{pmatrix}\epsilon_{x,t} \\ \epsilon_{y,t}\end{pmatrix}} \end{equation*}\]

con matriz de correlaciones de los errores reducidos

\[\begin{equation*} \Omega = E\left[\underset{\epsilon_t}{\begin{pmatrix}\epsilon_{x,t} \\ \epsilon_{y,t}\end{pmatrix}}\underset{\epsilon'_t}{\begin{pmatrix}\epsilon_{x,t} & \epsilon_{y,t}\end{pmatrix}}\right] = E\begin{pmatrix}\epsilon^2_{x,t} & \epsilon_{x,t}\epsilon_{y,t} \\ \epsilon_{y,t}\epsilon_{x,t} & \epsilon^2_{y,t}\end{pmatrix} = \begin{pmatrix}0.0400 & 0.0280 \\ 0.0280 & 0.0596\end{pmatrix} \end{equation*}\]

import numpy as np
import matplotlib.pyplot as plt
import seaborn
import pandas as pd
from statsmodels.tsa.api import VAR

Simulando los datos

Vamos a simular una muestra de 100 observaciones de un VAR(1). Empezamos por ingresar los valores de los parámetros

T = 100

A = np.array([[0.8, 0.7], [-0.2, 0.8]])
c = np.array([[0.9], [1.8]])

Ω = 0.04*np.array([[1, 0.7],[0.7,1.49]])

Calculamos la descomposición de Cholesky para poder simular la correlación de los errores

P = np.linalg.cholesky(Ω)
P

array([[0.2 , 0.  ],
       [0.14, 0.2 ]])

Fijamos una semilla para el generador de números aleatorios, para obtener resultados replicables.

np.random.seed(16)

Calculamos la media del proceso \(\mu = (I-A)^{1}c\) y lo usamos como valor inicial de la simulación.

𝜇 = (np.linalg.inv(np.eye(2) - A) @ c)

X = np.zeros((T,2))
X[0] = 𝜇.T

for t in range(1, T):
    X[t] = c.T + X[t-1] @ A.T + np.random.randn(2) @ P.T

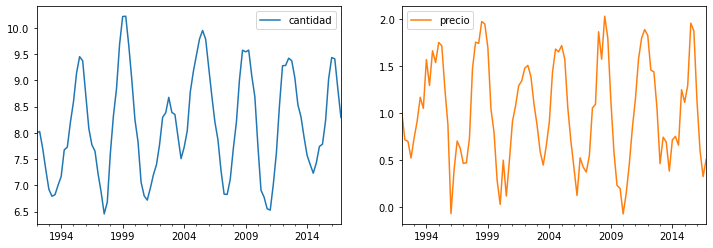
Guardamos los datos simulados como un DataFrame de pandas y los graficamos

trimestres = pd.date_range(start='1992q1', freq='Q', periods=T)
data = pd.DataFrame(X, columns=['cantidad', 'precio'], index=trimestres)

fig, axs = plt.subplots(1,2,figsize=[12,4])
data.plot(subplots=True, ax=axs);

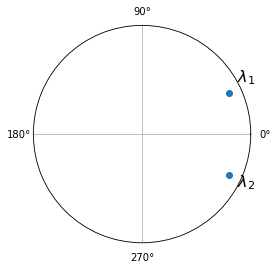
Determinando si el VAR es estable

Para ello calculamos los valores propios de la matriz A, y comprobamos si estan en el círculo unitario

eigenvalues = np.linalg.eigvals(A)
print('Los eigenvalores son ', eigenvalues)
print('y sus modulos son', abs(eigenvalues))

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, polar=True)

ax.plot(np.angle(eigenvalues), abs(eigenvalues),marker='o',linewidth=0)
ax.set(ylim=[0,1], yticks=[1], yticklabels=[''], xticks=np.arange(4)*np.pi/2)

ax.annotate('$\lambda_1$',[0.5,1.0], fontsize=16)
ax.annotate('$\lambda_2$',[-0.5,1.0], fontsize=16);

Los eigenvalores son  [0.8+0.37416574j 0.8-0.37416574j]
y sus modulos son [0.88317609 0.88317609]

Estimación del VAR a partir de los datos simulados

model = VAR(data)

Determinamos el rezago óptimo

model.select_order(5).summary()

VAR Order Selection (* highlights the minimums)

	AIC	BIC	FPE	HQIC
0	-1.168	-1.114	0.3110	-1.146
1	-6.478*	-6.316*	0.001537*	-6.412*
2	-6.460	-6.191	0.001566	-6.351
3	-6.389	-6.012	0.001681	-6.237
4	-6.359	-5.875	0.001733	-6.163
5	-6.311	-5.720	0.001819	-6.072

Estimamos el VAR con un único rezago

results = model.fit(maxlags=1)
results.summary()

  Summary of Regression Results   
==================================
Model:                         VAR
Method:                        OLS
Date:           Thu, 21, Jul, 2022
Time:                     00:08:37
--------------------------------------------------------------------
No. of Equations:         2.00000    BIC:                   -6.33706
Nobs:                     99.0000    HQIC:                  -6.43071
Log likelihood:           46.5202    FPE:                 0.00151202
AIC:                     -6.49434    Det(Omega_mle):      0.00142439
--------------------------------------------------------------------
Results for equation cantidad
==============================================================================
                 coefficient       std. error           t-stat            prob
------------------------------------------------------------------------------
const               0.822641         0.155447            5.292           0.000
L1.cantidad         0.808834         0.019385           41.726           0.000
L1.precio           0.731017         0.034625           21.112           0.000
==============================================================================

Results for equation precio
==============================================================================
                 coefficient       std. error           t-stat            prob
------------------------------------------------------------------------------
const               1.918492         0.211180            9.085           0.000
L1.cantidad        -0.222922         0.026335           -8.465           0.000
L1.precio           0.895834         0.047039           19.044           0.000
==============================================================================

Correlation matrix of residuals
            cantidad    precio
cantidad    1.000000  0.592419
precio      0.592419  1.000000

Pruebas de causalidad de Granger

En ambos casos, las pruebas confirman que una variable tiene capacidad predictiva sobre la otra variable.

results.test_causality('precio', 'cantidad').summary()

Granger causality F-test. H_0: cantidad does not Granger-cause precio. Conclusion: reject H_0 at 5% significance level.

Test statistic	Critical value	p-value	df
71.66	3.890	0.000	(1, 192)

results.test_causality('cantidad', 'precio').summary()

Granger causality F-test. H_0: precio does not Granger-cause cantidad. Conclusion: reject H_0 at 5% significance level.

Test statistic	Critical value	p-value	df
445.7	3.890	0.000	(1, 192)

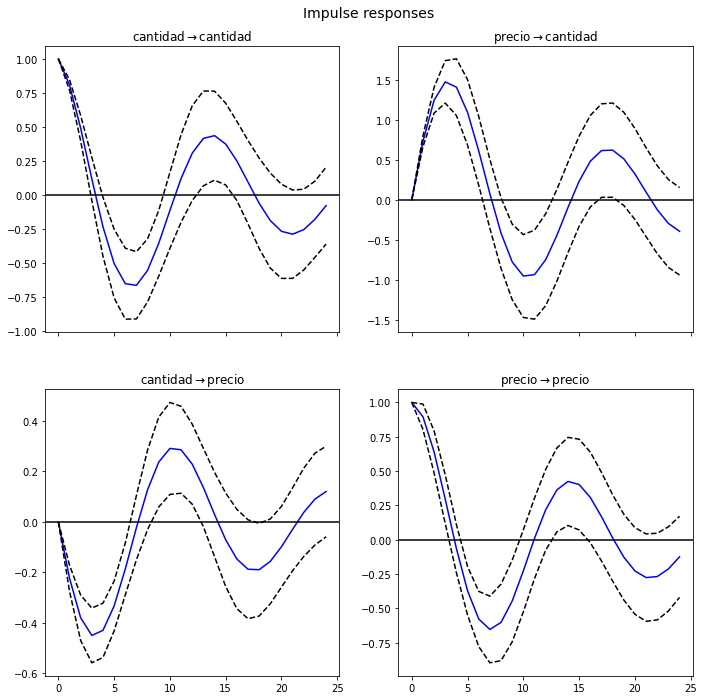
Funciones de impulso respuesta

Simulamos impulsos unitarios. A la izquierda, el impulso es \(\begin{pmatrix}1 \\ 0\end{pmatrix}\) (un choque de una unidad en la cantidad); a la derecha el impulso es \(\begin{pmatrix}0 \\ 1\end{pmatrix}\) (un choque de una unidad en el precio).

results.irf(24).plot();

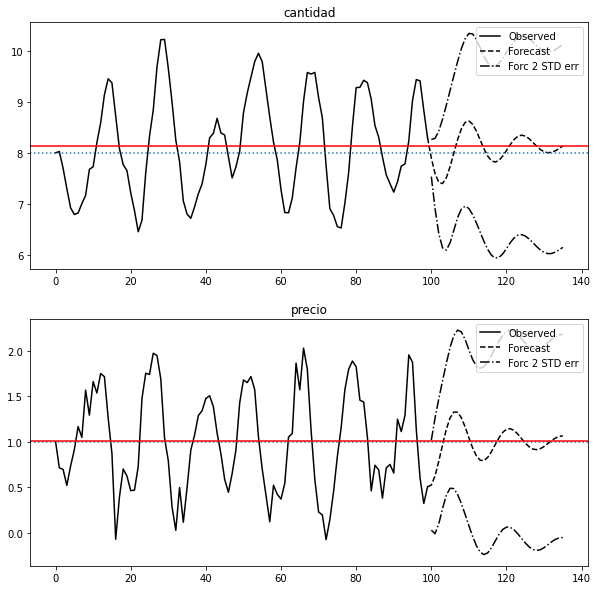
Pronosticando los siguientes datos

Vemos que después de un tiempo los pronósticos convergen a la media estimada del proceso (en rojo).

fig = results.plot_forecast(36)

for i in range(2):
    fig.axes[i].axhline(𝜇[i], ls=':')
    fig.axes[i].axhline(results.mean()[i], color='r')