1.5. Cálculo de transformaciones de la serie del PIB de Costa Rica#

Nota Para ejecutar este cuaderno se requiere el paquete bccr.

Cargar paquetes necesarios#

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from bccr import SW
plt.style.use('seaborn')

figpath = '../figures/'

Importar los datos#

pib = SW(PIB=33438)
pib /=1e6

def figura(datos, titulo, y, archivo=None):
    fig, ax = plt.subplots(1,1, figsize=[9,2.5])
    datos.plot(ax=ax, legend="")
    ax.set(title=titulo, ylabel=y, xlabel="")
    if archivo:
        fig.savefig(figpath + archivo + ".pdf", bbox_inches='tight')
    
    return ax

Graficar las series transformadas#

Nivel de la serie#

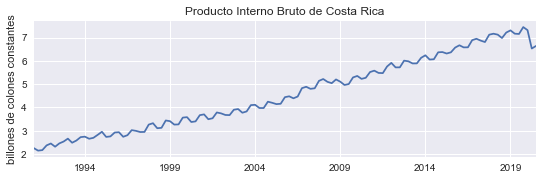
  • Antes de modelar una serie de tiempo, es útil representarla con un gráfico para detectar algunas de sus propiedades.

  • En este caso: el PIB

    • muestra una tendencia positiva

    • tiene variaciones estacionarias

  • En lo que sigue, nos referimos a esta serie en nivel como \(y_t\).

figura(pib, 'Producto Interno Bruto de Costa Rica', 'billones de colones constantes', 'pib');
../_images/Transforme_8_0.png

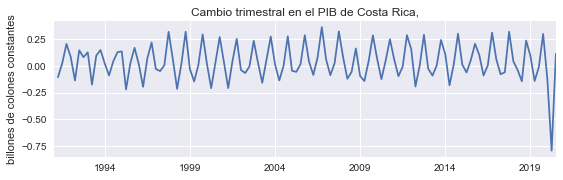
Primera diferencia de la serie#

\[\begin{equation*} \Delta y_t \equiv y_t - y_{t-1} \end{equation*}\]

  • Esta transformación

    • elimina la tendencia de la serie,

    • mantiene las oscilaciones estacionales.

figura(pib.diff(1), 'Cambio trimestral en el PIB de Costa Rica,','billones de colones constantes', 'd_pib');
../_images/Transforme_10_0.png

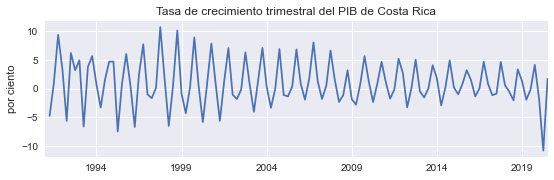
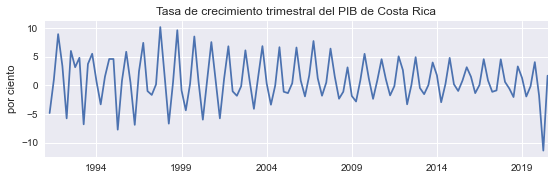
Tasa de crecimiento de la serie#

\[\begin{equation*} \Delta\% y_t \equiv \frac{y_t - y_{t-1}}{y_{t-1}} \times 100 \end{equation*}\]

  • Elimina tendencia, mantiene estacionalidad.

  • Limitación: asimetría con respecto a cambios positivos y negativos: Subir de 100 a 125 (aumento de 25%), bajar de 125 a 100 (caída de “solo” 20%).

figura(100*pib.pct_change(1), 'Tasa de crecimiento trimestral del PIB de Costa Rica', 'por ciento', 'dpc_pib');
../_images/Transforme_12_0.png

Tasa “continua” de crecimiento de la serie#

\[\begin{equation*} \Delta\% y_t \approx \left(\ln y_t - \ln y_{t-1}\right)\times 100 \end{equation*}\]

  • Similar a la anterior porque \(\ln(1+x)\approx x\) si \(x\) es “pequeño”

  • Ventaja: simetría con respecto a cambios positivos y negativos

figura(100*np.log(pib).diff(), 'Tasa de crecimiento trimestral del PIB de Costa Rica', 'por ciento', 'dlog_pib');
../_images/Transforme_14_0.png

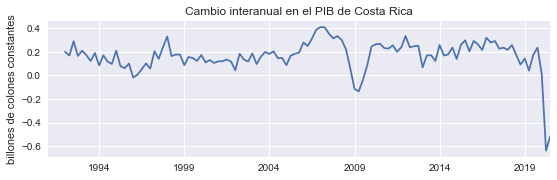
Diferencia interanual de la serie#

\[\begin{equation*} \Delta_4 y_t \equiv y_t - y_{t-4} \end{equation*}\]

  • Elimina tanto la tendencia como el componente estacional

  • Nótese la fuerte disminución del PIB durante la crisis de 2008.

figura(pib.diff(4), 'Cambio interanual en el PIB de Costa Rica','billones de colones constantes', 'd4_pib');
../_images/Transforme_16_0.png

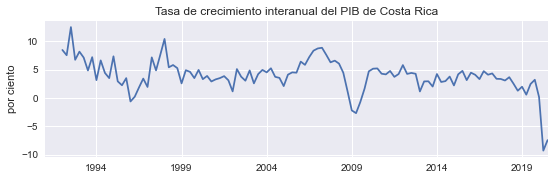
Tasa de crecimiento interanual#

\[\begin{equation*} \Delta_4\% y_t \approx \left(\ln y_t - \ln y_{t-4}\right)\times 100 \end{equation*}\]

  • Equivalente a la suma de las tasas de crecimiento de los cuatro trimestres comprendidos en el año:

\[\begin{align*} \Delta_4\% y_t &\approx \left(\ln y_t - \ln y_{t-4}\right)\times 100 \\ &= \left(\ln y_{t} - \ln y_{t-1} + \ln y_{t-1} - \ln y_{t-2} + \ln y_{t-2} - \ln y_{t-3} + \ln y_{t-3} - \ln y_{t-4}\right)\times 100 \\ &= \Delta\% y_{t} + \Delta\% y_{t-1} + \Delta\% y_{t-2} + \Delta\% y_{t-3} \end{align*}\]
figura(100*np.log(pib).diff(4), 'Tasa de crecimiento interanual del PIB de Costa Rica', 'por ciento', 'd4pc_pib');
../_images/Transforme_18_0.png

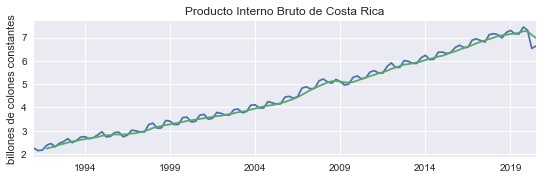
Serie suavizada por media móvil#

\[\begin{equation*} y^s_t \equiv \tfrac{1}{4}\left(y_t + y_{t-1} + y_{t-2} + y_{t-3}\right) \end{equation*}\]

  • Elimina el componente estacional, pero manteniendo la tendencia

  • Se observa un cambio estructural en 2008-2009.

pib2 = pd.concat([pib, pib.rolling(4).mean()], axis=1)
pib2.columns = ['Serie original', 'Serie suavizada']
figura(pib2, 'Producto Interno Bruto de Costa Rica', 'billones de colones constantes', 'pib_ma');
../_images/Transforme_20_0.png