4.5. Pruebas de raíz unitaria para el PIB en Costa Rica

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import statsmodels.api as sm

from statsmodels.tsa.stattools import adfuller, kpss

plt.style.use('seaborn')
plt.rc('figure', figsize=(15,4))
plt.rc('axes', titlesize=20, labelsize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=14)
plt.rc('ytick', labelsize=14)

figpath = "../figures/"

Descargar los datos

import bccr

pib = bccr.SW(PIB=33783)
pib['lPIB'] = np.log(pib['PIB'])

temp = pib.copy()
temp.index = pib.index.to_series().astype(str)
temp.reset_index().to_stata('pib-costa-rica.dta')
del temp

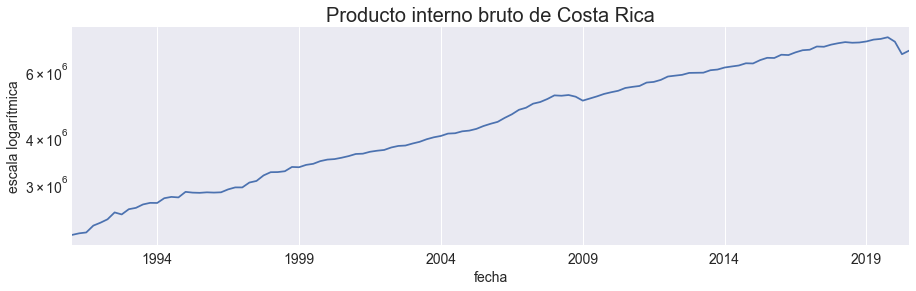
Gráfico de la serie

fig, ax = plt.subplots()
pib['PIB'].plot(ax=ax, legend=False)
ax.set(yscale='log', title='Producto interno bruto de Costa Rica', ylabel='escala logarítmica')
fig.savefig(figpath + 'pib-costa-rica-I(1).pdf', bbox_inches='tight')

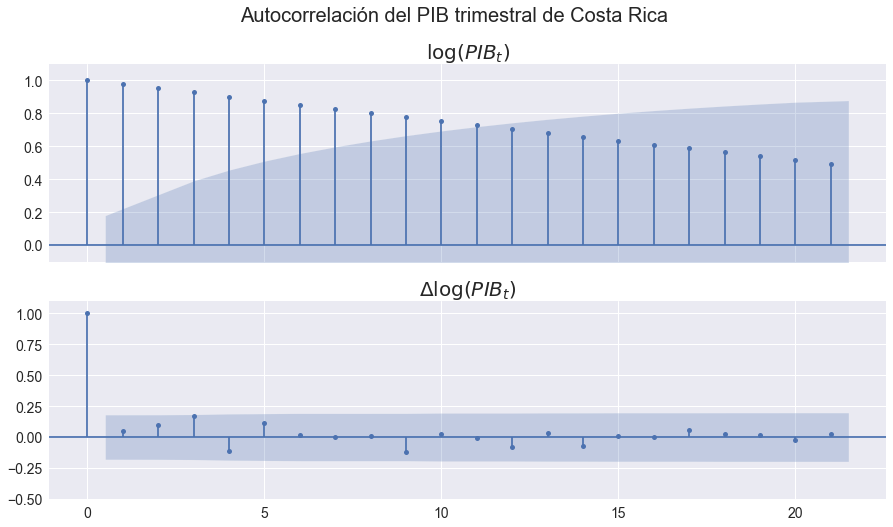
Correlograma del (logaritmo) del PIB y su primer diferencia

fig,axs = plt.subplots(2,1, figsize=[15,8], sharex=True)
sm.graphics.tsa.plot_acf(pib['lPIB'],ax=axs[0]);
axs[0].set(ylim=[-0.1,1.1], title='$\log(PIB_t)$')

sm.graphics.tsa.plot_acf(pib['lPIB'].diff().dropna(),ax=axs[1]);
axs[1].set(ylim=[-0.5,1.1], title='$\Delta\log(PIB_t)$')

fig.suptitle('Autocorrelación del PIB trimestral de Costa Rica', fontsize=20)
fig.savefig(figpath + 'pib-costa-rica-rho.pdf',bbox_inches='tight')

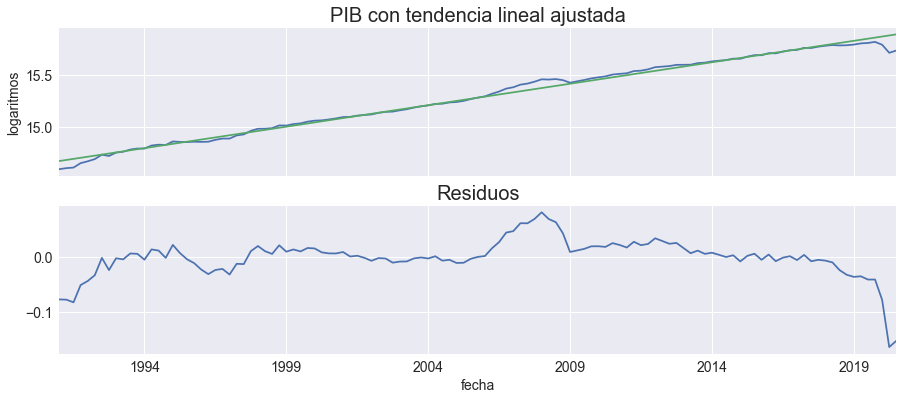
Ajustando una tendencia lineal

Estimando la tendencia y los residuos

pib['t'] = np.arange(pib.shape[0])

pib['tendencia'] = smf.ols('lPIB ~ t', pib).fit().fittedvalues
pib['residuos'] = pib['lPIB'] - pib['tendencia']

fig, axs = plt.subplots(2,1, figsize=[15,6], sharex=True)
pib[['lPIB','tendencia']].plot(ax=axs[0], legend=False)
axs[0].set(title='PIB con tendencia lineal ajustada', ylabel='logaritmos')

pib[['residuos']].plot(ax=axs[1], legend=False)
axs[1].set(title='Residuos')
fig.savefig(figpath + 'pib-tendencia-lineal.pdf', bbox_inches='tight')

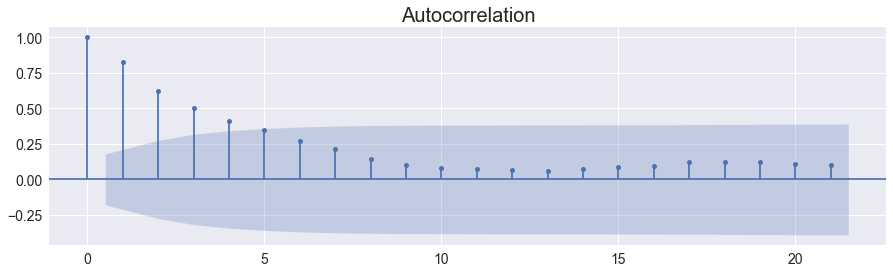
Correlograma de los residuos

sm.graphics.tsa.plot_acf(pib['residuos']);

Pruebas de DickeyFuller

Implementando la prueba DF con regresión lineal

dy  = pib['lPIB'].diff()[1:]
ly = pib['lPIB'].shift(1)[1:]
tt = np.arange(dy.size)

X = sm.add_constant(ly)
Z = np.c_[X,tt]

tnc = sm.OLS(dy,ly, hasconst=False).fit().tvalues[0]
tc = sm.OLS(dy, X, hasconst=True).fit().tvalues[1]
tct = sm.OLS(dy, Z, hasconst=True).fit().tvalues[1]

tnc, tc, tct

(7.591019301133945, -2.8373335086898184, -0.1961570690538992)

tbl = sm.OLS(dy, X, hasconst=True).fit().summary().tables[1]

with open(figpath + 'df-lpib-regresion.tex','w') as cuadro:
    cuadro.write(tbl.as_latex_tabular())

Implementando el código para hacer las tablas

specs = ['nc', 'c', 'ct']
indice = ['sin constante', 'con constante', 'con constante y tendencia']

def DF(datos, spec):
    res = adfuller(datos, maxlag=0,regression=spec)
    resultado = {
        'z':res[0], 
        '1%': res[4]['1%'], 
        '5%': res[4]['5%'], 
        '10%': res[4]['10%']}
    return resultado

def ADF(datos, spec):
    res = adfuller(datos, regression=spec, autolag='t-stat')
    resultado = {
        'z':res[0], 
        '1%': res[4]['1%'], 
        '5%': res[4]['5%'], 
        '10%': res[4]['10%'],
        'p': res[2]}
    return resultado

pruebas = {'df':DF, 'adf':ADF}

def tabla_dickey_fuller(serie, test, diff=0):
    datos = pib[serie].diff(diff) if diff else pib[serie]
    resultados = pd.DataFrame([pruebas[test](datos.dropna(), ss) for ss in specs], index=indice).round(3)
    nombre = '_'.join([test,serie,str(diff)])
    resultados.to_latex(figpath + nombre + '.tex')
    return resultados

Pruebas para serie en nivel

tabla_dickey_fuller('lPIB','df')

	z	1%	5%	10%
sin constante	7.591	-2.585	-1.943	-1.615
con constante	-2.837	-3.487	-2.886	-2.580
con constante y tendencia	-0.196	-4.038	-3.448	-3.149

Pruebas para serie en primer diferencia

tabla_dickey_fuller('lPIB', 'df', diff=1)

	z	1%	5%	10%
sin constante	-7.289	-2.585	-1.944	-1.615
con constante	-10.191	-3.488	-2.887	-2.580
con constante y tendencia	-10.859	-4.038	-3.449	-3.149

Serie de los residuos alrededor de tendencia

tabla_dickey_fuller('residuos', 'df', diff=0)

	z	1%	5%	10%
sin constante	-0.408	-2.585	-1.943	-1.615
con constante	-0.386	-3.487	-2.886	-2.580
con constante y tendencia	-0.196	-4.038	-3.448	-3.149

Prueba aumentada de Dickey-Fuller

Serie en nivel

tabla_dickey_fuller('lPIB', 'adf', diff=0)

	z	1%	5%	10%	p
sin constante	2.405	-2.586	-1.944	-1.615	4
con constante	-2.080	-3.492	-2.888	-2.581	9
con constante y tendencia	0.605	-4.044	-3.452	-3.151	9

Serie en primer diferencia

tabla_dickey_fuller('lPIB', 'adf', diff=1)

	z	1%	5%	10%	p
sin constante	-2.247	-2.585	-1.944	-1.615	2
con constante	-2.663	-3.492	-2.888	-2.581	8
con constante y tendencia	-3.338	-4.044	-3.452	-3.151	8

Serie de los residuos alrededor de tendencia

tabla_dickey_fuller('residuos', 'adf', diff=0)

	z	1%	5%	10%	p
sin constante	-0.211	-2.587	-1.944	-1.615	9
con constante	0.061	-3.492	-2.888	-2.581	9
con constante y tendencia	0.605	-4.044	-3.452	-3.151	9

Pruebas KPSS

def KPSS_una_serie(datos, tipo):
    return [kpss(datos.dropna(), regression=tipo, lags=k)[0] for k in range(7)]   

critical = pd.DataFrame(
    {'c': np.array([0.347, 0.463, 0.574, 0.739]),
     'ct':np.array([0.119, 0.146, 0.176, 0.216])},
    index=['10%', '5%', '2.5%', '1%'])

def tabla_KPSS(diff=0):
    datos = pib['lPIB'].diff(diff) if diff else pib['lPIB']
    resultados = pd.DataFrame([KPSS_una_serie(datos, ss) for ss in ['c','ct']], index=['c','ct']).round(3)
    #nombre = '_'.join([test,serie,str(diff)])
    #resultados.to_latex(figpath + nombre + '.tex')
    return resultados.T

%%capture
tab = pd.concat([tabla_KPSS(diff=r) for r in range(2)], axis=1,keys=['nivel','diferencia'])

tab.to_latex(figpath + 'kpss_lPIB.tex')
tab

	nivel		diferencia
	c	ct	c	ct
0	11.868	1.261	0.710	0.100
1	6.005	0.692	0.678	0.103
2	4.040	0.502	0.630	0.100
3	3.058	0.405	0.568	0.092
4	2.468	0.347	0.555	0.093
5	2.076	0.308	0.531	0.091
6	1.795	0.280	0.514	0.090

critical.to_latex(figpath + 'kpss_critical.tex')