Importando y manipulando datos con Python#

Ejemplo 1: Importando datos de Internet#

A menudo necesitamos darle seguimiento a algunos indicadores económicos. Este trabajo usualmente requiere:

visitar el sitio de Internet del proveedor de datos,
buscar los indicadores requeridos,
descargar los datos (posiblemente en varios archivos separados),
copiar los datos a un solo archivo,
acomodar los datos de manera apropiada,
y solo después de que se hayan completado estas engorrosas tareas, graficarlos.

Si este trabajo debe realizarse periódicamente entonces también se hace necesario documentar exhaustivamente cada uno de estos pasos, de manera que podamos replicarlos de manera exacta en un futuro. Sobra decir que, si estas tareas hay que realizarlas para múltiples indicadores, el trabajo termina demandando una cantidad de tiempo considerable y además es muy susceptible a errores.

Para facilitar este trabajo, podemos utilizar Python para descargar datos disponibles en Internet directamente, gracias a paquetes como pandas-datareader. Esto se hace fácilmente cuando los proveedores de datos proporcionan una API (interfaz de programa de aplicación) que especifica cómo un lenguaje como Python puede encontrar los datos deseados.

Vamos a ilustrar esto con un ejemplo. Supongamos que queremos datos recientes sobre el crecimiento económico para los países miembros de la CMCA. El Banco Mundial proporciona los datos pertinentes en su “World Database”, que podemos leer con el módulo wb de pandas_datareader.

import pandas as pd
from pandas_datareader import wb
import matplotlib.pyplot as plt

pd.set_option('display.precision',2)
%matplotlib inline

Para poder descargar datos del Banco Mundial, primero necesitamos saber el código exacto del indicador que queremos leer. La primera vez que hagamos esta tarea no conoceremos este código, pero podemos buscarlo en el sitio web del Banco Mundial o más fácilmente desde python. Por ejemplo, para encontrar datos sobre el PIB real per cápita, ejecutamos la función .search():

wb.search('gdp.*capita.*const')

	id	name	source	sourceNote	sourceOrganization	topics
716	6.0.GDPpc_constant	GDP per capita, PPP (constant 2011 internation...	LAC Equity Lab	GDP per capita based on purchasing power parit...	b'World Development Indicators (World Bank)'	Economy & Growth
10522	NY.GDP.PCAP.KD	GDP per capita (constant 2015 US$)	World Development Indicators	GDP per capita is gross domestic product divid...	b'World Bank national accounts data, and OECD ...	Economy & Growth
10524	NY.GDP.PCAP.KN	GDP per capita (constant LCU)	World Development Indicators	GDP per capita is gross domestic product divid...	b'World Bank national accounts data, and OECD ...	Economy & Growth
10526	NY.GDP.PCAP.PP.KD	GDP per capita, PPP (constant 2017 internation...	World Development Indicators	GDP per capita based on purchasing power parit...	b'International Comparison Program, World Bank...	Economy & Growth
10527	NY.GDP.PCAP.PP.KD.87	GDP per capita, PPP (constant 1987 internation...	WDI Database Archives		b''

wb.search('gdp.*capita.*const').iloc[:,:2]

	id	name
716	6.0.GDPpc_constant	GDP per capita, PPP (constant 2011 internation...
10522	NY.GDP.PCAP.KD	GDP per capita (constant 2015 US$)
10524	NY.GDP.PCAP.KN	GDP per capita (constant LCU)
10526	NY.GDP.PCAP.PP.KD	GDP per capita, PPP (constant 2017 internation...
10527	NY.GDP.PCAP.PP.KD.87	GDP per capita, PPP (constant 1987 internation...

donde el punto seguido de un asterisco .* indica que cualquier texto en esa posición es una coincidencia. Esta función devuelve una tabla de datos con información sobre indicadores que coinciden con los criterios de búsqueda. En la línea anterior, usamos el código .iloc[:,:2] para que Python solo imprima las dos primeras columnas de esa tabla.

Después de ejecutar esa búsqueda, elegimos el 'NY.GDP.PCAP.KD', cuya descripción es “GDP per capita (constant 2010 US$)”. Definimos una variable con una lista de códigos de país de los países del CMCA:

paises = ['CR', 'DO', 'GT', 'HN', 'NI', 'SV']

y procedemos a leer datos desde 1991:

datos = wb.download(indicator='NY.GDP.PCAP.KD',
                    country=paises,start=1991, end=2019)

datos.head(7)

		NY.GDP.PCAP.KD
country	year
Costa Rica	2019	12755.17
	2018	12573.96
	2017	12375.92
	2016	12004.67
	2015	11642.78
	2014	11355.33
	2013	11090.09

datos

		NY.GDP.PCAP.KD
country	year
Costa Rica	2019	12755.17
	2018	12573.96
	2017	12375.92
	2016	12004.67
	2015	11642.78
...	...	...
El Salvador	1995	2839.21
	1994	2743.37
	1993	2654.52
	1992	2542.90
	1991	2409.03

174 rows × 1 columns

También es posible leer datos de más de un indicador en una sola llamada a la función wb.download(), escribiendo sus códigos en una lista (tal como lo hicimos para leer datos de los seis países a la vez). En cualquier caso, obtenemos una tabla de datos en formato de panel, donde cada columna corresponde a uno de los indicadores.

Para nuestro ejemplo en particular, donde solo leemos un indicador, sería útil si la tabla estuviera organizada de manera que cada fila corresponda a un año y cada columna a un país. Podemos lograrlo con esta instrucción:

paises2 = {'Costa Rica':'CR', 
           'Dominican Republic':'DO',
           'El Salvador':'SV',
           'Guatemala':'GT',
           'Honduras':'HN',
           'Nicaragua':'NI'}

datos.unstack('country')

	NY.GDP.PCAP.KD
country	Costa Rica	Dominican Republic	El Salvador	Guatemala	Honduras	Nicaragua
year
1991	6018.86	2774.25	2409.03	2758.68	1633.67	1227.51
1992	6403.78	3028.11	2542.90	2817.23	1684.63	1204.88
1993	6683.84	3191.60	2654.52	2854.13	1744.26	1173.79
1994	6811.11	3216.11	2743.37	2896.22	1699.27	1187.29
1995	6920.58	3340.04	2839.21	2965.89	1753.86	1232.30
1996	6846.36	3480.27	2831.39	2981.12	1736.24	1285.78
1997	7053.14	3727.80	2891.60	3038.71	1764.74	1312.94
1998	7389.05	3915.14	2941.94	3115.98	1776.76	1338.66
1999	7538.89	4083.64	2981.34	3160.08	1714.96	1409.77
2000	7678.49	4209.41	2992.90	3195.39	1790.36	1444.93
2001	7805.31	4249.10	2999.32	3192.31	1790.80	1465.72
2002	7940.43	4375.79	3028.55	3239.57	1810.47	1455.85
2003	8157.65	4255.77	3059.57	3250.84	1845.64	1472.02
2004	8395.40	4304.77	3071.55	3282.32	1913.11	1529.17
2005	8606.33	4647.04	3140.03	3320.16	1980.99	1573.03
2006	9109.53	5006.55	3261.76	3427.68	2062.60	1616.06
2007	9725.38	5308.63	3308.05	3573.60	2141.38	1674.92
2008	10052.68	5409.95	3364.10	3620.83	2183.77	1708.82
2009	9837.88	5393.47	3280.02	3570.30	2086.27	1630.09
2010	10236.98	5771.92	3334.93	3606.43	2120.74	1679.03
2011	10559.21	5881.14	3447.35	3688.87	2159.71	1761.22
2012	10945.04	5969.35	3528.87	3731.68	2207.23	1850.69
2013	11090.09	6187.28	3591.43	3802.15	2228.15	1916.28
2014	11355.33	6547.31	3636.01	3903.06	2256.02	1981.75
2015	11642.78	6921.52	3705.58	3994.64	2302.20	2049.85
2016	12004.67	7300.03	3781.38	4034.16	2351.09	2115.95
2017	12375.92	7556.85	3846.97	4091.27	2423.59	2185.89
2018	12573.96	7997.76	3920.53	4160.07	2475.17	2086.01
2019	12755.17	8314.34	3993.53	4254.04	2499.49	1982.63

datos.unstack('country').columns

MultiIndex([('NY.GDP.PCAP.KD',         'Costa Rica'),
            ('NY.GDP.PCAP.KD', 'Dominican Republic'),
            ('NY.GDP.PCAP.KD',        'El Salvador'),
            ('NY.GDP.PCAP.KD',          'Guatemala'),
            ('NY.GDP.PCAP.KD',           'Honduras'),
            ('NY.GDP.PCAP.KD',          'Nicaragua')],
           names=[None, 'country'])

datos.unstack('country')

	NY.GDP.PCAP.KD
country	Costa Rica	Dominican Republic	El Salvador	Guatemala	Honduras	Nicaragua
year
1991	6018.86	2774.25	2409.03	2758.68	1633.67	1227.51
1992	6403.78	3028.11	2542.90	2817.23	1684.63	1204.88
1993	6683.84	3191.60	2654.52	2854.13	1744.26	1173.79
1994	6811.11	3216.11	2743.37	2896.22	1699.27	1187.29
1995	6920.58	3340.04	2839.21	2965.89	1753.86	1232.30
1996	6846.36	3480.27	2831.39	2981.12	1736.24	1285.78
1997	7053.14	3727.80	2891.60	3038.71	1764.74	1312.94
1998	7389.05	3915.14	2941.94	3115.98	1776.76	1338.66
1999	7538.89	4083.64	2981.34	3160.08	1714.96	1409.77
2000	7678.49	4209.41	2992.90	3195.39	1790.36	1444.93
2001	7805.31	4249.10	2999.32	3192.31	1790.80	1465.72
2002	7940.43	4375.79	3028.55	3239.57	1810.47	1455.85
2003	8157.65	4255.77	3059.57	3250.84	1845.64	1472.02
2004	8395.40	4304.77	3071.55	3282.32	1913.11	1529.17
2005	8606.33	4647.04	3140.03	3320.16	1980.99	1573.03
2006	9109.53	5006.55	3261.76	3427.68	2062.60	1616.06
2007	9725.38	5308.63	3308.05	3573.60	2141.38	1674.92
2008	10052.68	5409.95	3364.10	3620.83	2183.77	1708.82
2009	9837.88	5393.47	3280.02	3570.30	2086.27	1630.09
2010	10236.98	5771.92	3334.93	3606.43	2120.74	1679.03
2011	10559.21	5881.14	3447.35	3688.87	2159.71	1761.22
2012	10945.04	5969.35	3528.87	3731.68	2207.23	1850.69
2013	11090.09	6187.28	3591.43	3802.15	2228.15	1916.28
2014	11355.33	6547.31	3636.01	3903.06	2256.02	1981.75
2015	11642.78	6921.52	3705.58	3994.64	2302.20	2049.85
2016	12004.67	7300.03	3781.38	4034.16	2351.09	2115.95
2017	12375.92	7556.85	3846.97	4091.27	2423.59	2185.89
2018	12573.96	7997.76	3920.53	4160.07	2475.17	2086.01
2019	12755.17	8314.34	3993.53	4254.04	2499.49	1982.63

GDP = datos.unstack('country')['NY.GDP.PCAP.KD']
GDP

country	Costa Rica	Dominican Republic	El Salvador	Guatemala	Honduras	Nicaragua
year
1991	6018.86	2774.25	2409.03	2758.68	1633.67	1227.51
1992	6403.78	3028.11	2542.90	2817.23	1684.63	1204.88
1993	6683.84	3191.60	2654.52	2854.13	1744.26	1173.79
1994	6811.11	3216.11	2743.37	2896.22	1699.27	1187.29
1995	6920.58	3340.04	2839.21	2965.89	1753.86	1232.30
1996	6846.36	3480.27	2831.39	2981.12	1736.24	1285.78
1997	7053.14	3727.80	2891.60	3038.71	1764.74	1312.94
1998	7389.05	3915.14	2941.94	3115.98	1776.76	1338.66
1999	7538.89	4083.64	2981.34	3160.08	1714.96	1409.77
2000	7678.49	4209.41	2992.90	3195.39	1790.36	1444.93
2001	7805.31	4249.10	2999.32	3192.31	1790.80	1465.72
2002	7940.43	4375.79	3028.55	3239.57	1810.47	1455.85
2003	8157.65	4255.77	3059.57	3250.84	1845.64	1472.02
2004	8395.40	4304.77	3071.55	3282.32	1913.11	1529.17
2005	8606.33	4647.04	3140.03	3320.16	1980.99	1573.03
2006	9109.53	5006.55	3261.76	3427.68	2062.60	1616.06
2007	9725.38	5308.63	3308.05	3573.60	2141.38	1674.92
2008	10052.68	5409.95	3364.10	3620.83	2183.77	1708.82
2009	9837.88	5393.47	3280.02	3570.30	2086.27	1630.09
2010	10236.98	5771.92	3334.93	3606.43	2120.74	1679.03
2011	10559.21	5881.14	3447.35	3688.87	2159.71	1761.22
2012	10945.04	5969.35	3528.87	3731.68	2207.23	1850.69
2013	11090.09	6187.28	3591.43	3802.15	2228.15	1916.28
2014	11355.33	6547.31	3636.01	3903.06	2256.02	1981.75
2015	11642.78	6921.52	3705.58	3994.64	2302.20	2049.85
2016	12004.67	7300.03	3781.38	4034.16	2351.09	2115.95
2017	12375.92	7556.85	3846.97	4091.27	2423.59	2185.89
2018	12573.96	7997.76	3920.53	4160.07	2475.17	2086.01
2019	12755.17	8314.34	3993.53	4254.04	2499.49	1982.63

GDP.rename(columns=paises2, inplace=True)
GDP

country	CR	DO	SV	GT	HN	NI
year
1991	6018.86	2774.25	2409.03	2758.68	1633.67	1227.51
1992	6403.78	3028.11	2542.90	2817.23	1684.63	1204.88
1993	6683.84	3191.60	2654.52	2854.13	1744.26	1173.79
1994	6811.11	3216.11	2743.37	2896.22	1699.27	1187.29
1995	6920.58	3340.04	2839.21	2965.89	1753.86	1232.30
1996	6846.36	3480.27	2831.39	2981.12	1736.24	1285.78
1997	7053.14	3727.80	2891.60	3038.71	1764.74	1312.94
1998	7389.05	3915.14	2941.94	3115.98	1776.76	1338.66
1999	7538.89	4083.64	2981.34	3160.08	1714.96	1409.77
2000	7678.49	4209.41	2992.90	3195.39	1790.36	1444.93
2001	7805.31	4249.10	2999.32	3192.31	1790.80	1465.72
2002	7940.43	4375.79	3028.55	3239.57	1810.47	1455.85
2003	8157.65	4255.77	3059.57	3250.84	1845.64	1472.02
2004	8395.40	4304.77	3071.55	3282.32	1913.11	1529.17
2005	8606.33	4647.04	3140.03	3320.16	1980.99	1573.03
2006	9109.53	5006.55	3261.76	3427.68	2062.60	1616.06
2007	9725.38	5308.63	3308.05	3573.60	2141.38	1674.92
2008	10052.68	5409.95	3364.10	3620.83	2183.77	1708.82
2009	9837.88	5393.47	3280.02	3570.30	2086.27	1630.09
2010	10236.98	5771.92	3334.93	3606.43	2120.74	1679.03
2011	10559.21	5881.14	3447.35	3688.87	2159.71	1761.22
2012	10945.04	5969.35	3528.87	3731.68	2207.23	1850.69
2013	11090.09	6187.28	3591.43	3802.15	2228.15	1916.28
2014	11355.33	6547.31	3636.01	3903.06	2256.02	1981.75
2015	11642.78	6921.52	3705.58	3994.64	2302.20	2049.85
2016	12004.67	7300.03	3781.38	4034.16	2351.09	2115.95
2017	12375.92	7556.85	3846.97	4091.27	2423.59	2185.89
2018	12573.96	7997.76	3920.53	4160.07	2475.17	2086.01
2019	12755.17	8314.34	3993.53	4254.04	2499.49	1982.63

GDP.index = pd.period_range(start=GDP.index[0], periods=len(GDP.index),freq='A')

Una vez que los datos se organizan de esta manera, es muy fácil calcular el crecimiento para todos los países en un solo paso:

GDP.tail(6)

country	CR	DO	SV	GT	HN	NI
2014	11355.33	6547.31	3636.01	3903.06	2256.02	1981.75
2015	11642.78	6921.52	3705.58	3994.64	2302.20	2049.85
2016	12004.67	7300.03	3781.38	4034.16	2351.09	2115.95
2017	12375.92	7556.85	3846.97	4091.27	2423.59	2185.89
2018	12573.96	7997.76	3920.53	4160.07	2475.17	2086.01
2019	12755.17	8314.34	3993.53	4254.04	2499.49	1982.63

GROWTH = 100 * GDP.dropna().pct_change()
GROWTH.tail()

country	CR	DO	SV	GT	HN	NI
2015	2.53	5.72	1.91	2.35	2.05	3.44
2016	3.11	5.47	2.05	0.99	2.12	3.22
2017	3.09	3.52	1.73	1.42	3.08	3.31
2018	1.60	5.83	1.91	1.68	2.13	-4.57
2019	1.44	3.96	1.86	2.26	0.98	-4.96

o para generar una tabla de datos formateada para ser incluida en un documento $\LaTeX$

GROWTH.tail(6).round(2).to_latex('micuadro.tex')

En la última instrucción, la parte .tail(6) indica que solo queremos las últimas seis observaciones, mientras que la parte .to_latex('micuadro.tex') exporta esa tabla a un archivo llamado micuadro.tex, que luego puede incluirse en un documento. El resultado de este código es

print(open('micuadro.tex').read())

\begin{tabular}{lrrrrrr}
\toprule
country &    CR &    DO &    SV &    GT &    HN &    NI \\
\midrule
2014 &  2.39 &  5.82 &  1.24 &  2.65 &  1.25 &  3.42 \\
2015 &  2.53 &  5.72 &  1.91 &  2.35 &  2.05 &  3.44 \\
2016 &  3.11 &  5.47 &  2.05 &  0.99 &  2.12 &  3.22 \\
2017 &  3.09 &  3.52 &  1.73 &  1.42 &  3.08 &  3.31 \\
2018 &  1.60 &  5.83 &  1.91 &  1.68 &  2.13 & -4.57 \\
2019 &  1.44 &  3.96 &  1.86 &  2.26 &  0.98 & -4.96 \\
\bottomrule
\end{tabular}

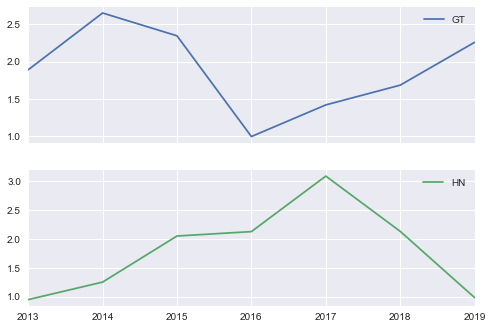
Finalmente, graficamos los resultados. Es posible mejorar el aspecto estético de esta figura, por ejemplo, cambiando la posición de la leyenda. Tales mejoras no se presentan aquí por consideraciones de espacio.

GROWTH.head()

country	CR	DO	SV	GT	HN	NI
1991	NaN	NaN	NaN	NaN	NaN	NaN
1992	6.40	9.15	5.56	2.12	3.12	-1.84
1993	4.37	5.40	4.39	1.31	3.54	-2.58
1994	1.90	0.77	3.35	1.47	-2.58	1.15
1995	1.61	3.85	3.49	2.41	3.21	3.79

paises

['CR', 'DO', 'GT', 'HN', 'NI', 'SV']

plt.style.use('seaborn');
GROWTH = GROWTH[paises]

GROWTH[['GT','HN']]['2013':].plot(subplots=True)
plt.savefig('growth.pdf', bbox_inches='tight')

../../_images/Python-09--manipulando-datos_33_0.png

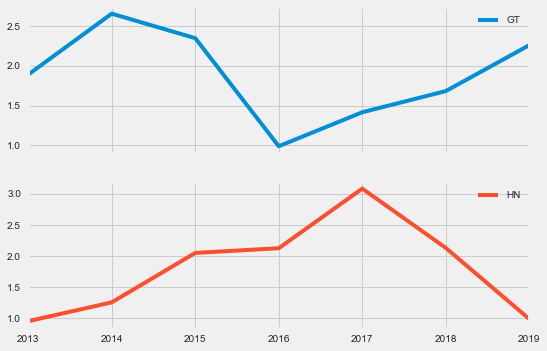
plt.style.use('fivethirtyeight');
GROWTH.columns = paises
GROWTH[['GT','HN']]['2013':].plot(subplots=True)

array([<AxesSubplot:>, <AxesSubplot:>], dtype=object)

../../_images/Python-09--manipulando-datos_34_1.png

También es posible trazar cada una de las series de tiempo en un subgráfico separado, con la instrucción

GROWTH.plot(subplots=True, layout=[2,3], sharey=True);
#plt.savefig('growth-subplots.pdf', bbox_inches='tight')

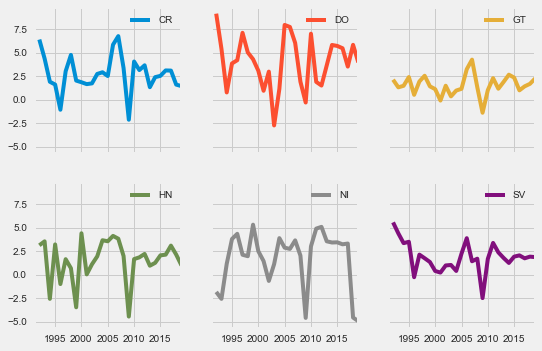
../../_images/Python-09--manipulando-datos_36_0.png

donde hemos especificado que cada serie de tiempo debe trazarse por separado (subplots=True), organizarse en dos filas y tres columnas (layout=[2,3]), y todos los subgráficos deben tener el mismo eje “y” (sharey=True, para facilitar las comparaciones de países).

Para ver cuáles estilos de gráficos están disponibles

plt.style.available

['Solarize_Light2',
 '_classic_test_patch',
 '_mpl-gallery',
 '_mpl-gallery-nogrid',
 'bmh',
 'classic',
 'dark_background',
 'fast',
 'fivethirtyeight',
 'ggplot',
 'grayscale',
 'seaborn',
 'seaborn-bright',
 'seaborn-colorblind',
 'seaborn-dark',
 'seaborn-dark-palette',
 'seaborn-darkgrid',
 'seaborn-deep',
 'seaborn-muted',
 'seaborn-notebook',
 'seaborn-paper',
 'seaborn-pastel',
 'seaborn-poster',
 'seaborn-talk',
 'seaborn-ticks',
 'seaborn-white',
 'seaborn-whitegrid',
 'tableau-colorblind10']

Ejemplo 2: Estimaciones econométricas#

El paquete statsmodels de Python permite la estimación de muchos tipos de modelos econométricos, aunque no tantos como se pueden estimar usando R. Una ilustración simple es la estimación de una función de consumo keynesiana,

\[\begin{equation*} \ln(c_t) = \beta_0 + \beta_1 \ln(y_t) + \epsilon_t \end{equation*}\]

donde $c_t$ representa consumo, $y_t$ ingreso, $\epsilon$ un shock estocástico. En este caso $\beta_1$ corresponde a la elasticidad ingreso del consumo.

Al igual que en el ejemplo anterior, usaremos pandas-datareader para importar datos de Internet. En este ejemplo, también importamos la función log() del paquete numpy para calcular el logaritmo de los datos, así como el módulo formula.api de statsmodels para estimar el modelo.

import pandas_datareader.data as web
from numpy import log
import statsmodels.formula.api as smf

Una vez hecho esto, estamos listos para importar datos. En este ejemplo, utilizamos datos trimestrales sobre consumo y producción en los Estados Unidos, disponibles en FRED, una base de datos del Banco de la Reserva Federal de Saint Louis. Para “consumo” usamos la serie “PCEC” (Personal Consumption Expenditures), y para “ingreso” usamos “GDP” (Gross Domestic Product).

usdata = web.DataReader(['PCEC','GDP'],'fred', 1947, 2018)

usdata.tail()

	PCEC	GDP
DATE
2017-01-01	13046.44	19153.91
2017-04-01	13144.40	19322.92
2017-07-01	13268.15	19558.69
2017-10-01	13497.45	19882.97
2018-01-01	13667.43	20143.72

Después de ejecutar esta instrucción, la variable usdata apunta a una tabla de datos pandas, en la que cada columna corresponde a una variable y cada fila a un cuarto.

Ahora estimamos el modelo por mínimos cuadrados ordinarios (.ols()) e imprimimos un resumen de los resultados

log(usdata).plot()

<AxesSubplot:xlabel='DATE'>

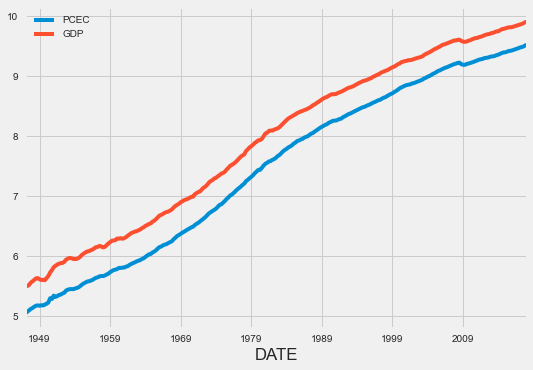
../../_images/Python-09--manipulando-datos_47_1.png

mod = smf.ols('PCEC ~ GDP', log(usdata)).fit()
mod.summary()

OLS Regression Results
Dep. Variable:	PCEC	R-squared:	1.000
Model:	OLS	Adj. R-squared:	1.000
Method:	Least Squares	F-statistic:	6.309e+05
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	0.00
Time:	00:18:31	Log-Likelihood:	592.46
No. Observations:	285	AIC:	-1181.
Df Residuals:	283	BIC:	-1174.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	-0.6745	0.010	-64.899	0.000	-0.695	-0.654
GDP	1.0273	0.001	794.300	0.000	1.025	1.030

Omnibus:	51.744	Durbin-Watson:	0.073
Prob(Omnibus):	0.000	Jarque-Bera (JB):	86.528
Skew:	1.022	Prob(JB):	1.62e-19
Kurtosis:	4.764	Cond. No.	47.1

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Observe que la función .ols() toma dos argumentos, la fórmula que especifica el modelo y el nombre de la tabla de datos que contiene las variables. En este bloque de código, especificamos los datos como log(usdata), que le dice a Python que queremos el logaritmo de los datos, lo que nos ahorra la tarea de generar otra tabla de datos con los datos transformados de antemano (como sería necesario en, para ejemplo, Stata).

Alternativamente, esa línea también se puede escribir como

mod = smf.ols('log(PCEC) ~ log(GDP)', usdata).fit()

lo cual es conveniente en casos donde no todas las variables deben ser transformadas.

Como se espera en una regresión de series de tiempo de tendencia, el estadístico $R^2$ es muy cercano a uno, y el estadístico de Durbin-Watson apunta a la alta posibilidad de autocorrelación en los residuos. Este documento no pretende ser una guía de mejores prácticas en econometría, pero consideremos un último modelo en el que el crecimiento del consumo depende del crecimiento del ingreso:

\[\begin{equation*} \Delta\ln(c_t) = \beta_0 + \beta_1 \Delta \ln(y_t) + \epsilon_t \end{equation*}\]

que estimamos en Python con

smf.ols('PCEC ~ GDP', log(usdata).diff()).fit().summary()

OLS Regression Results
Dep. Variable:	PCEC	R-squared:	0.492
Model:	OLS	Adj. R-squared:	0.490
Method:	Least Squares	F-statistic:	272.8
Date:	Thu, 21 Jul 2022	Prob (F-statistic):	2.49e-43
Time:	00:18:31	Log-Likelihood:	1011.9
No. Observations:	284	AIC:	-2020.
Df Residuals:	282	BIC:	-2012.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	0.0062	0.001	8.668	0.000	0.005	0.008
GDP	0.6167	0.037	16.515	0.000	0.543	0.690

Omnibus:	102.779	Durbin-Watson:	2.541
Prob(Omnibus):	0.000	Jarque-Bera (JB):	1098.030
Skew:	-1.129	Prob(JB):	3.68e-239
Kurtosis:	12.364	Cond. No.	91.4

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Notamos que ahora el $R^2$ ya no está cerca de uno, y que la estadística de Durbin-Watson está más cerca de 2.0, lo que indica falta de autocorrelación.

Con los resultados disponibles, podríamos predecir que un aumento de un punto porcentual (p.p.) en el crecimiento del PIB conduciría a un 0.618 p.p. aumento en el crecimiento del consumo. Sin embargo, dado que la muestra de datos cubre un período tan largo (casi 70 años de observación trimestral), es razonable preguntarse si los parámetros en este modelo son constantes, dado que podrían haber ocurrido varios cambios estructurales a lo largo de estos años. Una forma de evaluar dicha posibilidad es estimar el modelo con una muestra continua. En particular, vamos a estimar este modelo con 24 ventanas trimestrales de ventana móvil, cambiando la muestra en un cuarto en cada paso.

En este caso, dado que vamos a necesitar datos de crecimiento muchas veces, es más eficiente calcular los datos de crecimiento solo una vez y almacenarlos en una variable de ‘crecimiento’. Con el código [1:] estamos eliminando la primera observación, que perdemos cuando calculamos la diferencia de primer orden .diff(). Además, usamos la propiedad .shape de la tabla para averiguar cuántas observaciones tenemos T, y luego establecemos el rango de ventana en observaciones h = 24:

growth = (100*log(usdata).diff())[1:]
T, nvar = growth.shape
h = 40

T /4

71.0

Para facilitar el siguiente paso, definimos la función window_beta1, que toma como único argumento el número de la última observación que se incluirá en la estimación, y devuelve el valor del coeficiente estimado del PIB

def window_beta1(k):
    submuestra = growth[k-h:k]
    return smf.ols('PCEC~GDP', submuestra).fit().params['GDP']

window_beta1(81)

0.41460208327311915

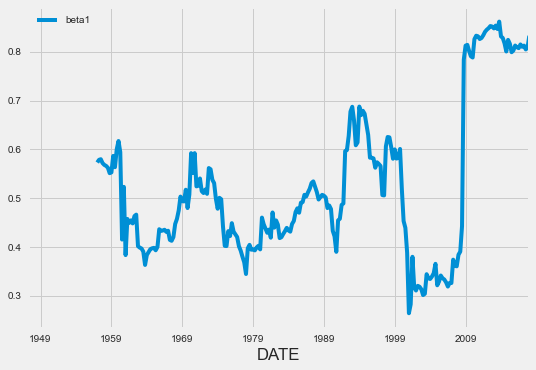
Con esto, estamos listos para estimar el modelo muchas veces, agregando los resultados a la tabla de growth como el “indicador” beta1. Al graficar los resultados, obtenemos la siguiente figura, donde vemos claramente que el efecto del crecimiento del PIB en el crecimiento del consumo es bastante inestable y, por lo tanto, las predicciones hechas con el modelo simple podrían ser muy pobres.

growth.loc[h-1:,'beta1'] = [window_beta1(k) for k in range(h,T+1)]
growth[['beta1']].plot()
#plt.savefig('dynamic-beta.pdf', bbox_inches='tight')

<AxesSubplot:xlabel='DATE'>

../../_images/Python-09--manipulando-datos_59_2.png

Referencias#

Romero-Aguilar, Randall (2017). Python para economistas. Nota Económica Regionales N0.93, diciembre. SECMCA.

Apuntes de Macroeconometría

Importando y manipulando datos con Python

Contents

Importando y manipulando datos con Python#

Ejemplo 1: Importando datos de Internet#

Ejemplo 2: Estimaciones econométricas#

Referencias#