1.4. Procesos estocásticos#

\[ \begin{align}\begin{aligned}\require{color} \newcommand{\alert}[1]{{\color{RedOrange} #1}} \newcommand{\notation}[2]{\underset{\color{MidnightBlue}\text{#2}}{#1}} \newcommand{\simbolo}[2]{\underset{\color{MidnightBlue}#2}{#1}} \newcommand{\notationbrace}[2]{{\underbrace{#1}_{\color{MidnightBlue}\text{#2}}}} \DeclareMathOperator{\dd}{\,d\!} \DeclareMathOperator{\E}{\mathbb{E}{}} \DeclareMathOperator{\Var}{Var{}} \DeclareMathOperator{\Cov}{Cov{}} \DeclareMathOperator{\Lag}{L{}} \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator{\Prob}{\mathbb{P}} \newcommand{\marginal}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\MAT}[1]{\begin{bmatrix} #1 \end{bmatrix}} \newcommand{\mat}[1]{\left[\begin{smallmatrix} #1 \end{smallmatrix}\right]}\\\begin{split}\DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\X}{\mathbf{x}} \DeclareMathOperator{\y}{\mathbf{y}} \DeclareMathOperator{\h}{\mathbf{h}} \newcommand{\stackEq}[1]{\MAT{#1_1 \\ #1_2 \\ \vdots \\ #1_M}} \newcommand{\e}{\mathbf{\epsilon}} \newcommand{\Y}{\mathbf{Y}} \newcommand{\estimator}[2]{{\hat{#1}^{\text{#2}}}} \newcommand{\estimate}[2]{\underset{(#2)}{#1}} \DeclareMathOperator{\plim}{plim} \newcommand{\PLIM}[2]{#1\xrightarrow{p} #2}\end{split}\end{aligned}\end{align} \]

Procesos estocásticos#

Un proceso estocástico es una secuencia temporal de variables aleatorias \(\{Y_t\}^\infty_{t=-\infty}\).

Dos tipos de procesos: Continuos ~ si sus realizaciones son tomadas de un intervalo de la recta real \(Y_t \in [a, b] \subseteq \mathbb{R}\).

Discretos

si hay solamente un número contable de realizaciones \(Y_t \in \{y_1, y_2, \dots, y_n\}\).

También llamado proceso generador de datos.

Procesos estocásticos i.i.d.#

  • Los elementos de un proceso estocástico son idéntica e indepedientemente distribuidos (abreviado “iid”), si la distribución de probabilidad es la misma para cada miembro del proceso \(Z_t\) e independiente de las realizaciones de otros miembros del proceso.

  • En este caso, para la muestra \(\{Y_t\}^T_{t=1}\):

\[\begin{multline*} \Prob[Y_1 = y_1, Y_2 = y_2, \dots, Y_T = y_T] = \\ \Prob(Y_1 = y_1)\times \Prob(Y_2 = y_2)\times\dots\times\Prob(Y_T = y_T) \end{multline*}\]

Momentos incondicionales#

  • Función de distribución acumulada incondicional

    \[\begin{equation*} F_{Y_t}\left(y\right) = \Prob\left[Y_t\leq y\right] \end{equation*}\]

  • Esperanza (media) incondicional

    \[\begin{equation*} \mu_t\equiv \E\left(Y_t\right) = \int_{-\infty}^{\infty}y\dd F_{Y_t}\left(y\right) \end{equation*}\]

  • Varianza incondicional

    \[\begin{equation*} \gamma_{0t}\equiv \E\left(Y_t-\mu_t\right)^2 = \int_{-\infty}^{\infty}\left(y-\mu_t\right)^2 \dd F_{Y_t}\left(y\right) \end{equation*}\]

  • Autocovarianza

    \[\begin{equation*} \gamma_{jt}\equiv \E\left(Y_t-\mu_t\right)\left(Y_{t-j}-\mu_{t-j}\right) \end{equation*}\]

Estacionariedad#

Si la media \(\mu_t\) ni las autocovarianzas \(\gamma_{jt}\) dependen de la fecha \(t\), entonces decimos que el proceso \(Y_t\) es covarianza-estacionario o débilmente estacionario:

\[\begin{align*} \E\left(Y_t\right) &=\mu &\text{para todo } &t \\ \E\left(Y_t-\mu\right)\left(Y_{t-j}-\mu\right) &=\gamma_j &\text{para todo } &t \text{ y cualquier } j \end{align*}\]

Ejemplo 1.5 Procesos estacionarios y no estacionarios#

Supongamos que \(Y_t\) es un proceso estocástico tal que \(Y_t \sim N(\mu_t, \sigma^2_t)\)

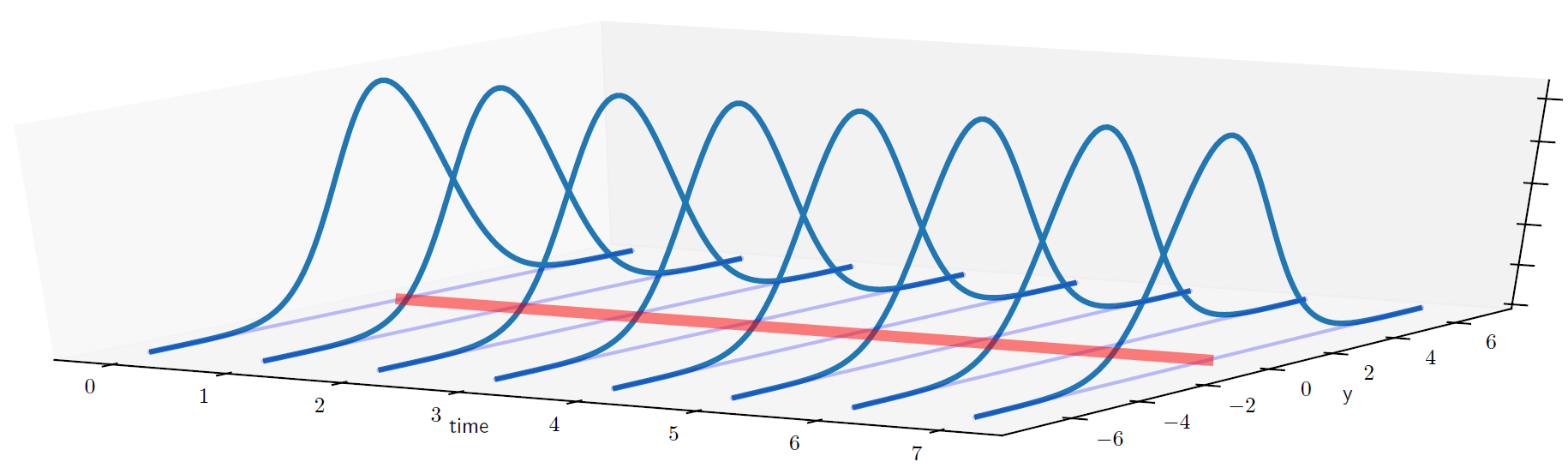
../../_images/stationary.png

Fig. 1.2 Estacionario porque \(\mu_t\) y \(\sigma^2_t\) son constantes “)#

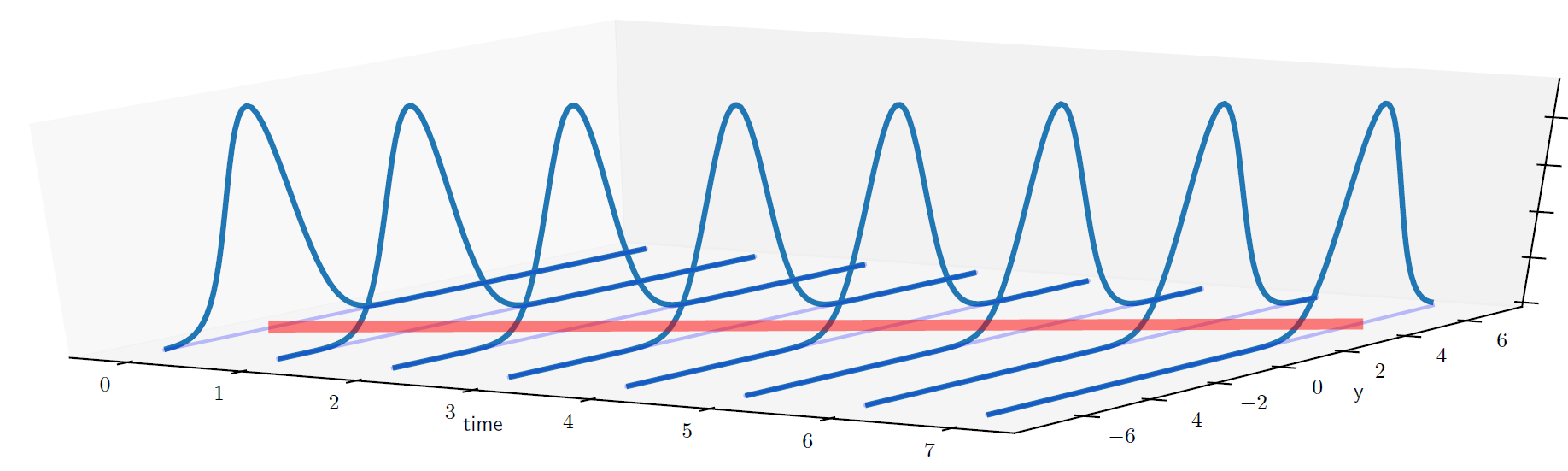
../../_images/trending.png

Fig. 1.3 No estacionario porque \(\mu_t\) está cambiando con el tiempo#

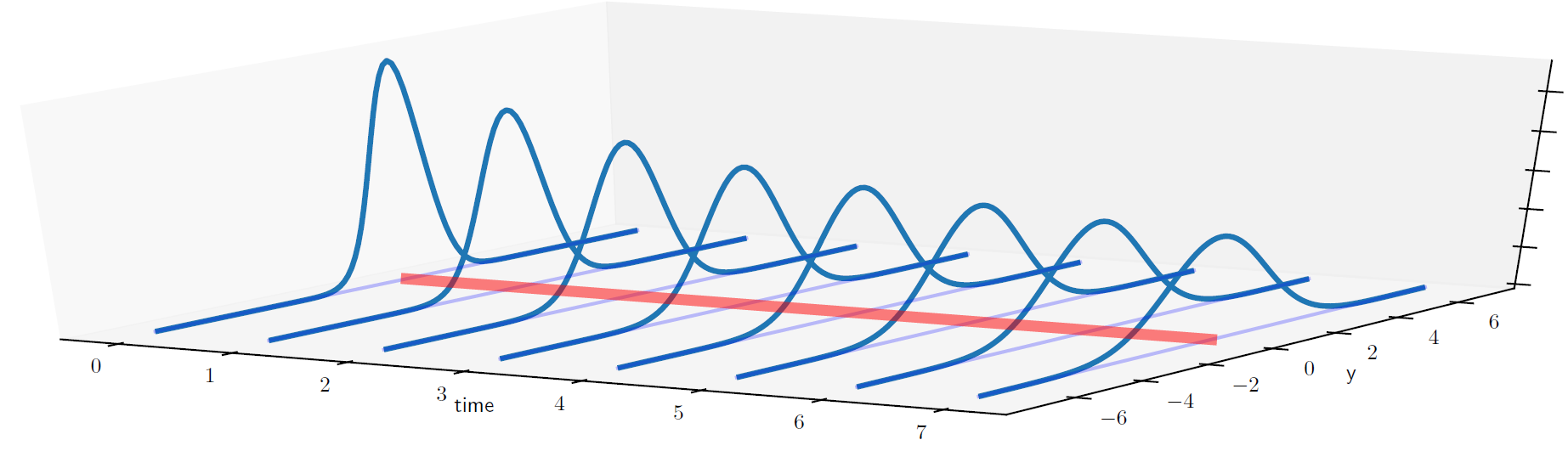
../../_images/widening.png

Fig. 1.4 No estacionario porque \(\sigma^2_t\) está cambiando con el tiempo#

Ruido blanco#

El bloque básico para construir los procesos considerados en este curso es una secuencia \(\left\{\epsilon_t\right\}\) cuyos elementos tienen media cero y varianza \(\sigma^2\),

\[\begin{align*} \E\left(\epsilon_t\right) &=0 & &\text{media cero} \\ \E\left(\epsilon^2_t\right) &=\sigma^2 & &\text{varianza constante} \\ \E\left(\epsilon_t\epsilon_\tau\right) &= 0 \quad\text{for }t\neq\tau & &\text{términos no correlacionados} \end{align*}\]

Si los términos están normalmente distribuidos

\[\begin{equation*} \epsilon_t \sim N(0,\sigma^2) \end{equation*}\]

entonces tenemos el proceso ruido blaco gaussiano.