El filtro de Hodrick y Prescott
Contents
import numpy as np
import pandas as pd
pd.options.plotting.backend = "plotly"
import pandas_datareader as pdr
4.5. El filtro de Hodrick y Prescott#
Otro método para remover una tendencia
Desagregación de una serie de tiempo#
Tenemos una muestra de \(T\) observaciones de la variable aleatoria \(Y_t\):
\(Y_t\) tiene dos componentes: crecimiento (tendencia) \(s_t\) y ciclo \(c_t\).
Asumimos que la tendencia es una curva suave, aunque no necesariamente una línea recta.
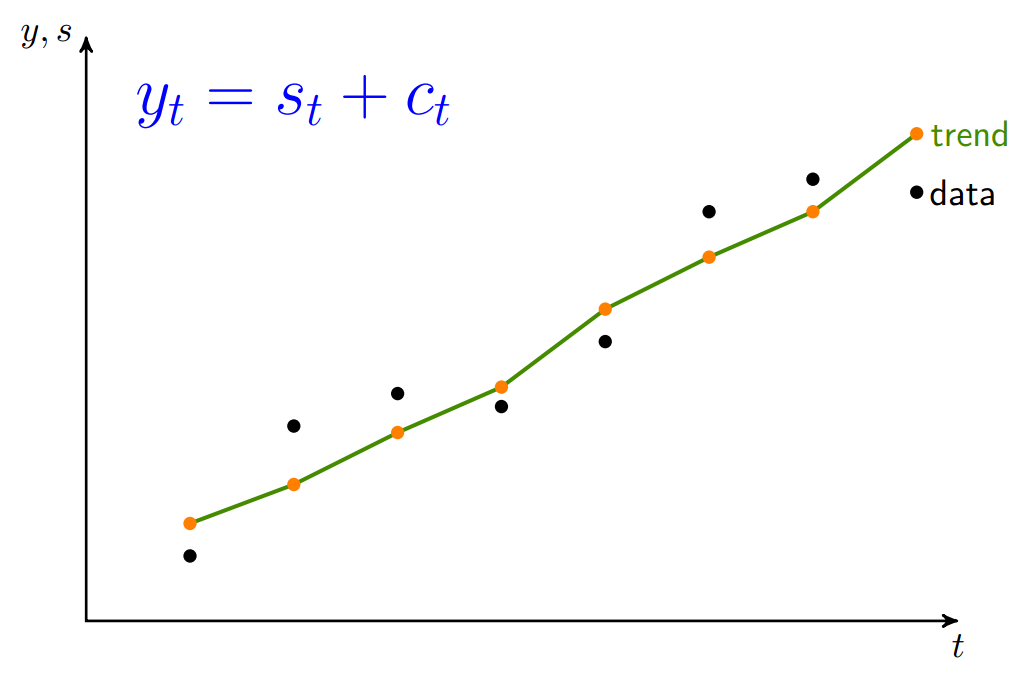
Objetivos en conflicto#
Partiendo de \(y_t\), \cite{Hodrick-Prescott:1997} “extraen” la tendencia \(s_t\)
tratando de balancear dos objetivos mutuamente excluyentes:
el ajuste a los datos originales, es decir, \(y_t-s_t\) debe ser pequeño.
la tendencia resultante debe ser suaver, por lo que los cambios de pendiente \((s_{t+1}-s_t)-(s_t-s_{t-1})\) también deben ser pequeños.
La importancia relativa de estos dos factores es ponderada con el parámetro \(\lambda\).
El filtro de Hodrick y Prescott#
Formalmente, la tendencia la definen por:
Un truco de álgebra lineal#
Definimos las matrices
Reescribimos el problema de optimización
Resolviendo el problema#
Las condiciones de primer orden son
Por lo que el filtro HP es
Observe que cada dato de tendencia \(s_t\) es simplemente un promedio ponderado de todos los datos en \(Y\). Además. algunas de las ponderaciones son negativas!
Por otra parte, los datos del ciclo \(C=\left[c_1,c_2,c_3,c_4,c_5\right]'\) están dados por:
De nuevo, observe que cada dato del ciclo \(c_t\) es un promedio ponderado de todos los puntos en \(Y\), pero donde las ponderaciones suman cero.
Escogiendo \(\lambda\)#
El resultado del filtro es muy sensible a la escogencia de \(\lambda\). Como regla habitual, \(\lambda\) se escoge según la frecuencia de los datos
Anuales \(\Rightarrow 100\)
Trimestrales \(\Rightarrow 1600\)
Mensuales \(\Rightarrow 14400\)
def HP_filter(y: pd.Series, 𝜆: float):
"""
Obtiene la tendencia y ciclo según filtro de Hodrick-Prescott
A la serie se le calcula el logaritmo
:param x: datos originales
:param 𝜆: parámetro de suavizamiento de la tendencia
:return: un pd.DataFrame con la serie original, la tendencia, y el ciclo
"""
y.dropna(inplace=True)
T = y.shape[0]
A = np.zeros((T-2, T))
for i in range(T-2):
A[i, i:i+3] = 1, -2, 1
B = np.identity(T) + 𝜆 * (A.T @ A)
tendencia = np.exp(np.linalg.solve(B, np.log(y)))
ciclo = 100 * (y/tendencia - 1) # como desviación porcentual respecto de la tendencia
return pd.DataFrame(
{'serie original': y,
'tendencia': tendencia,
'ciclo': ciclo
},
index = y.index)
gdp = pdr.get_data_fred('GDPC1', start=1947)
gdp = HP_filter(gdp['GDPC1'], 𝜆=1600)
gdp[['serie original', 'tendencia']].plot(title="Serie desestacionalizada y su tendencia")
gdp[['ciclo']].plot(title="Ciclo del PIB, como % de desviación")
Fuente de datos: https://fred.stlouisfed.org/series/GDPC1/
El filtro HP tiene malas propiedades estadísticas#
\cite{Hamilton:2017}: Why You Should Never Use the HP Filter?
El filtro Hodrick-Prescott introduce relaciones dinámicas espurias que no tienen sustento en el proceso generador de datos subyacente.
Los valores filtrados al final de la muestra son muy distintos de los del medio, y también están caracterizados por una dinámica espuria.
Una formalización estadística del problema típicamente produce valores de \(\lambda\) que distan mucho de los usados comúnmente en la práctica.
Para Hamilton, hay una alternativa mejor: una regresión AR(4) alcanza todos los objetivos buscados por usuarios del filtro HP pero con ninguno de sus desventajas.
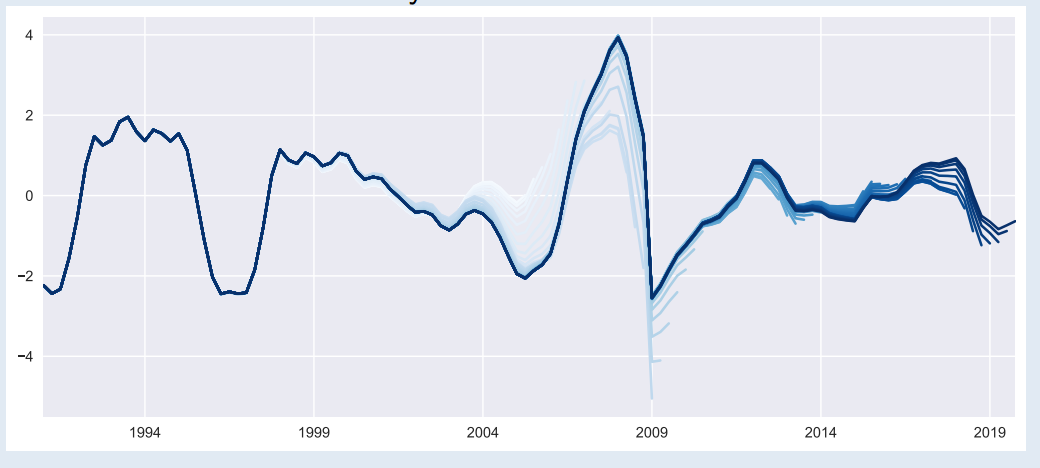
Fig. 4.1 Ciclo del PIB de Costa Rica, conforme se van agregando nuevas observaciones#
HP puede inducir conclusiones equivocadas acerca del comovimiento de series#
\textcite{CogleyNason:1995} analizaron las propiedades espectrales del filtro HP
Cuando se mide el componente cíclico de una serie de tiempo, ¿es buena idea usar el filtro HP?
Depende de la serie original
Sí, si es estacionaria alrededor de tendencia
No, si es estacionaria en diferencia
Este resultado tiene implicaciones importantes para modelos DSGE: Cuando se aplica el filtro HP a una serie integrada, el filtro introduce periodicidad y comovimiento en las frecuencias del ciclo económico, aún si no estaban presentes en los datos originales.


